- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Discussions
Solve problems, and share tips and tricks with other JMP users.- JMP User Community
- :
- Discussions
- :
- Re: What is the intuitive explanation for wider confidence interval band in regr...
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
What is the intuitive explanation for wider confidence interval band in regression?
Hello,
We can easily find that the confidence interval for the regression gets wider than the center from the following equation: 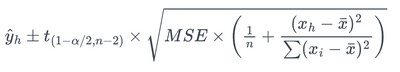
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: What is the intuitive explanation for wider confidence interval band in regression?
I see the need to modify my post. First, context matters. How was the data collected? This can have an effect on interpretation. I am trying to provide an intuitive explanation, not a technically correct explanation. If you notice the squared term in the equation. The farther away from the mean the greater the uncertainty (by uncertainty, I mean the dictionary definition not MSE), hence the wider the confidence intervals. Given there is uncertainty in the estimate of the mean (or Y intercept) and in the estimate of the slope of the regression line, as you get farther from the mean, the uncertainty in the estimation of the slope increases.
Intuitively think of these situations:
Imagine what happens to your confidence in predicting the weather in 1 hour vs. 24 hours vs. next week or
confidence in predicting traffic in the next block vs. 1 mile away vs. 100 miles away.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: What is the intuitive explanation for wider confidence interval band in regression?
A clarification: the uncertainty in the slope is constant. It is represented in two ways. The standard error of the estimate of the slope parameter indicates the expected variation in the estimate across all possible random samples of data of the same size from the same populations. The standard error can also indicate the uncertainty as a confidence interval of the slope estimate. Both representations are constant or independent of X.
The expression above is about the uncertainty in the estimated mean response assuming the model is correct and the variance of the response is independent of X. Notice MSE in the expression? It is a constant. It does not depend on X. If it did, then linear regression would be inappropriate and regression results would be misleading.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: What is the intuitive explanation for wider confidence interval band in regression?
I see the need to modify my post. First, context matters. How was the data collected? This can have an effect on interpretation. I am trying to provide an intuitive explanation, not a technically correct explanation. If you notice the squared term in the equation. The farther away from the mean the greater the uncertainty (by uncertainty, I mean the dictionary definition not MSE), hence the wider the confidence intervals. Given there is uncertainty in the estimate of the mean (or Y intercept) and in the estimate of the slope of the regression line, as you get farther from the mean, the uncertainty in the estimation of the slope increases.
Intuitively think of these situations:
Imagine what happens to your confidence in predicting the weather in 1 hour vs. 24 hours vs. next week or
confidence in predicting traffic in the next block vs. 1 mile away vs. 100 miles away.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: What is the intuitive explanation for wider confidence interval band in regression?
A clarification: the uncertainty in the slope is constant. It is represented in two ways. The standard error of the estimate of the slope parameter indicates the expected variation in the estimate across all possible random samples of data of the same size from the same populations. The standard error can also indicate the uncertainty as a confidence interval of the slope estimate. Both representations are constant or independent of X.
The expression above is about the uncertainty in the estimated mean response assuming the model is correct and the variance of the response is independent of X. Notice MSE in the expression? It is a constant. It does not depend on X. If it did, then linear regression would be inappropriate and regression results would be misleading.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: What is the intuitive explanation for wider confidence interval band in regression?
Point taken, the OP wants an intuitive explanation and I assume this means not the text book explanation. Perhaps I have failed in my attempt.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: What is the intuitive explanation for wider confidence interval band in regression?
You didn't fail! I just wanted to use clear and consistent terminology when someone is learning a concept for the first time. So many forks in the road...
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: What is the intuitive explanation for wider confidence interval band in regression?
As you sample more data and update your regression line, you will find that the vertical distance between the old and new regression line is largest at the ends and smallest at the centre. Thus it makes sense that the confidence band is wider at the ends.
Recommended Articles
- © 2026 JMP Statistical Discovery LLC. All Rights Reserved.
- Terms of Use
- Privacy Statement
- Contact Us

