- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Discussions
Solve problems, and share tips and tricks with other JMP users.- JMP User Community
- :
- Discussions
- :
- Re: What is k when assessing variable importance?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
What is k when assessing variable importance?
Hi JMP Community, I was running neural networks to construct prediction models by JMP and assessing variable importance by Dependent Resampled Inputs, which using a k-nearest neighbors approach. I had the variable importance for each variable in the model, but how can I know the value of k and the other details of the k-nearest neighbors approach?
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: What is k when assessing variable importance?
I do not think that the importance result is based on k. The help system says:
Factor values are constructed from observed combinations
using a k-nearest neighbors approach, in order to account for correlation. This option
treats observed variance and covariance as representative of the covariance structure for
your factors. Use this option when you believe that your factors are correlated. Note that
this option is sensitive to the number of rows in the data table. If used with a small number
of rows, the results can be unreliable.
Further:
Note: Variable importance indices are constructed using Monte Carlo sampling. For this reason, you can expect some variation in importance index values from one run to another.
In other words, a k-nearest neighbors approach is used to cluster observations so that the covariance structure of the data can be maintained. These observations are put into the model to get predicted values. Now, repeat (this is the Monte Carlo part) by choosing a new set of observations. See how much a change in a single factor made so that you can assess the importance of that variable.
I do not know all of the details of the k-nearest neighbors approach that is used, but I would guess that if a choice of k is made, it would be the one that describes the data the best. Look at the k-nearest neighbors clustering technique in the help section to see how JMP "optimally" chooses a k in that situation. If this approach is truly followed, I do not know what range of k is explored. Either way, I would bet that a range of k values are used due to the monte carlo simulation that is going on.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: What is k when assessing variable importance?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: What is k when assessing variable importance?
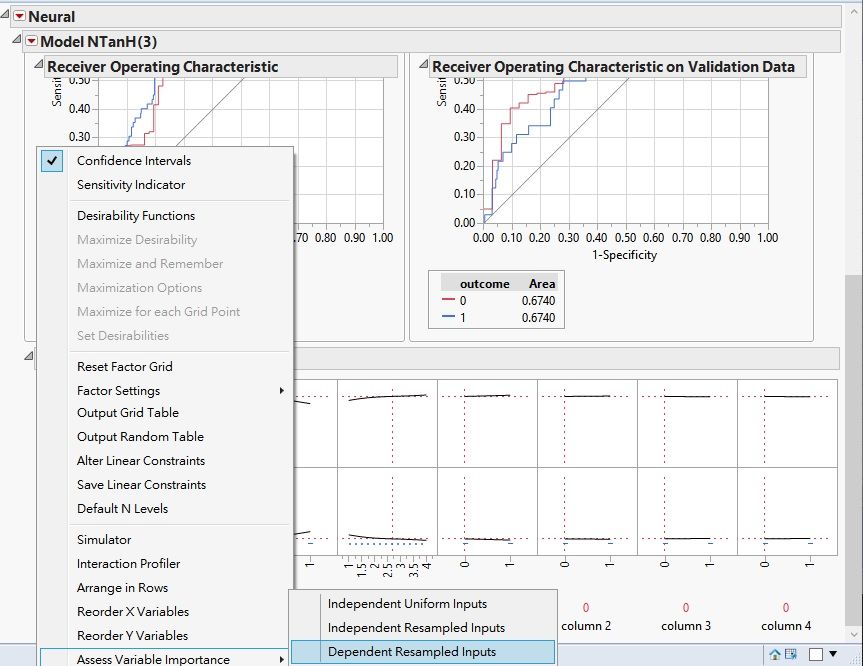
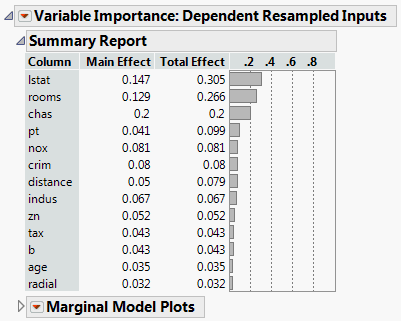
Thank you for replying. I did prediction model of neural network, I selected Profilers>Assess Variable Importance>Dependent Resampled Inputs, and will show a list of variable importance. According to the JMP Help, the importance was calculated using a k-nearest neighbors approach. My question is that if I can know the k value of this k-nearest neighbors approach?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: What is k when assessing variable importance?
Thank you for replying. I did prediction model of neural network, I selected Profilers>Assess Variable Importance>Dependent Resampled Inputs, and will show a list of variable importance. According to the JMP Help, the importance was calculated using a k-nearest neighbors approach. My question is that if I can know the k value of this k-nearest neighbors approach?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: What is k when assessing variable importance?
I do not think that the importance result is based on k. The help system says:
Factor values are constructed from observed combinations
using a k-nearest neighbors approach, in order to account for correlation. This option
treats observed variance and covariance as representative of the covariance structure for
your factors. Use this option when you believe that your factors are correlated. Note that
this option is sensitive to the number of rows in the data table. If used with a small number
of rows, the results can be unreliable.
Further:
Note: Variable importance indices are constructed using Monte Carlo sampling. For this reason, you can expect some variation in importance index values from one run to another.
In other words, a k-nearest neighbors approach is used to cluster observations so that the covariance structure of the data can be maintained. These observations are put into the model to get predicted values. Now, repeat (this is the Monte Carlo part) by choosing a new set of observations. See how much a change in a single factor made so that you can assess the importance of that variable.
I do not know all of the details of the k-nearest neighbors approach that is used, but I would guess that if a choice of k is made, it would be the one that describes the data the best. Look at the k-nearest neighbors clustering technique in the help section to see how JMP "optimally" chooses a k in that situation. If this approach is truly followed, I do not know what range of k is explored. Either way, I would bet that a range of k values are used due to the monte carlo simulation that is going on.
Recommended Articles
- © 2026 JMP Statistical Discovery LLC. All Rights Reserved.
- Terms of Use
- Privacy Statement
- Contact Us