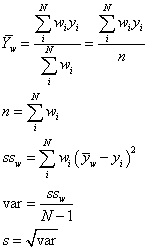- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Discussions
Solve problems, and share tips and tricks with other JMP users.- JMP User Community
- :
- Discussions
- :
- Weighted Standard Deviation
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Weighted Standard Deviation
Hi
How does JMP calculate a weighted standard deviation (when a variable is selected in the weighting tab in the Distribution Platform?
Thank you
Fanie
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Weighted Standard Deviation
It is not a matter of ignorance. There are at least four definitions of the weight standard deviation or variance. The definitions differ only in the denominator that is used. That is to say that the weighted mean and weight sum of squares are the same in all the definitions. JMP only implements one of the four definitions. Other software might implement this definition or one of the others.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Weighted Standard Deviation
The calculation is described here: weighted arithmetic mean. Use these formulas to understand the quantities in the results.
Use the script to illustrated the calculation steps. Open the Log before running the scripts.
Names Default to Here( 1 );
// open examle
dt = Open( "$SAMPLE_DATA/Big Class.jmp" );
dt << New Column( "Row Weight", Numeric, Continuous,
Values(
[0.466037725564092, 3.88878780649975, 2.4091640743427, 2.11785415420309,
4.79403748759069, 2.30050488375127, 1.58066931064241, 3.18035316769965,
1.57862229505554, 0.304837201256305, 3.91091752331704, 2.63118736562319,
3.27893625595607, 3.02616479573771, 1.75871466752142, 1.95901472005062,
1.4666282152757, 2.11275573237799, 2.02008433057927, 4.89492299617268,
0.493469994980842, 4.89886545110494, 2.22502982476726, 4.72375275800005,
0.830245516262948, 1.67820788919926, 3.44848407898098, 4.0259948768653,
3.2834971731063, 4.52901363372803, 3.88477634754963, 4.72076337435283,
4.64333190233447, 3.1073961337097, 0.579181439243257, 2.74820194579661,
0.191317443968728, 2.94498334173113, 2.51307534286752, 1.23225981369615]
)
);
// launch distribution analysis
biv = dt << Distribution(
Weight( :row weight ),
Continuous Distribution(
Column( :height ),
Customize Summary Statistics(
Sum Wgt( 1 ),
Variance( 1 ),
Corrected SS( 1 ),
Set Alpha Level( 0.05 )
)
),
SendToReport(
Dispatch( {}, "height", OutlineBox, {Set Title( "weighted height" )} )
)
);
// compute weight standard deviation and show intermediate results
y = :height << Get As Matrix; // data
w = :row weight << Get As Matrix; // weights
n = Sum( w ); // sum of weights
wYBar = (w`*y / n)[1]; // weighted average
ss = (w`*(y-wYBar)^2)[1]; // corrected weighted sum of squares
var = ss / (N Row( y )-1); // weighted variance, unbiased
s = Sqrt( var ); // weighted standard deviation
Show( wYbar, s, ss, var ); // view all results in Log
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Weighted Standard Deviation
HI Mark,
Thank you, I do appreciate your input.
So, I assume then the standard deviation printed in the distribution platform when a weight column property has been set should not be used?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Weighted Standard Deviation
Why do you assume that you should not use it?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Weighted Standard Deviation
Hi Mark,
I am drowning in my own ignorance...
I calculated the weighted mean of a dataset in Excel and compared it to JMP. The results did not match.
The formula I used in is:
This agrees with the code except:
var = ss / (N Row( y )-1); // weighted variance, unbiased should be:
var = ss / ((N Row( y )-1/N Row(y))*n; // weighted variance, unbiasedClearly I do not understand this.
Thank you
Fanie
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Weighted Standard Deviation
It is not a matter of ignorance. There are at least four definitions of the weight standard deviation or variance. The definitions differ only in the denominator that is used. That is to say that the weighted mean and weight sum of squares are the same in all the definitions. JMP only implements one of the four definitions. Other software might implement this definition or one of the others.
Recommended Articles
- © 2026 JMP Statistical Discovery LLC. All Rights Reserved.
- Terms of Use
- Privacy Statement
- Contact Us