- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Discussions
Solve problems, and share tips and tricks with other JMP users.- JMP User Community
- :
- Discussions
- :
- Re: Weighted Least Squares and Residuals
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Weighted Least Squares and Residuals
Attached is a sample of real estate sales and house sizes. If you build a model predicting price as a function of size, there is clear evidence of nonconstant variance. So, I created a weight column to do a weighted least squares regression. However, the residual pattern never changes - I tried weights = 1/size, then size squared, cubed, etc. The residual pattern appears exactly the same until I use the 5th power of the size - then the residuals become zero and the fit is perfect. I don't understand why 5th and higher powers on the residuals result in a perfect fit (though I suspect it is because the weights become so small that the regression line just becomes the mean price line and the errors are being ignored due to the tiny weights). But my real question is why the residual pattern remains unchanged even with weights of 1/size4.
In the attached data table, I put the script for the original, unweighted regression model. There are also scripts for the weighted regressions using the inverse of the 4th and 5th powers of the house size.
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Weighted Least Squares and Residuals
The residuals are not the same with weighting as they are without weighting, but the overall pattern is the same. You fit a linear model in both cases and even though the two sets of parameter estimates are not identical, you are still plotting actual price minus predicted price versus predicted price. The weights affect the parameter estimates, not the pattern of residuals.
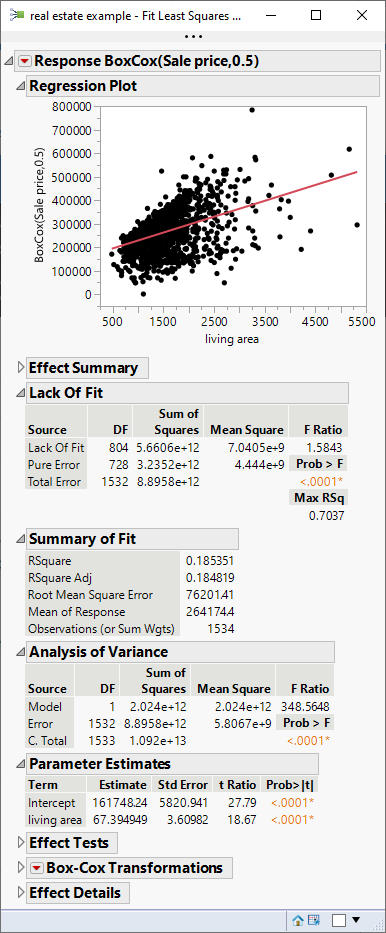
Weighting in this linear regression is by reciprocal variance, but the variance function might be difficult to determine in this case. So there are other techniques that can help. The first technique is to transform the response and therefore alter the variance. The Box-Cox transformation is used for several purposes, including stabilizing the response variance. The command is in the Factor Profiling sub-menu under the red triangle for Fit Least Squares. Here is the linear regression using the transformed response:
I didn't spend any time selecting the lambda parameter for the transformation, so you might do better with another value, but you can see that the residual pattern is different and getting closer to constant variance.
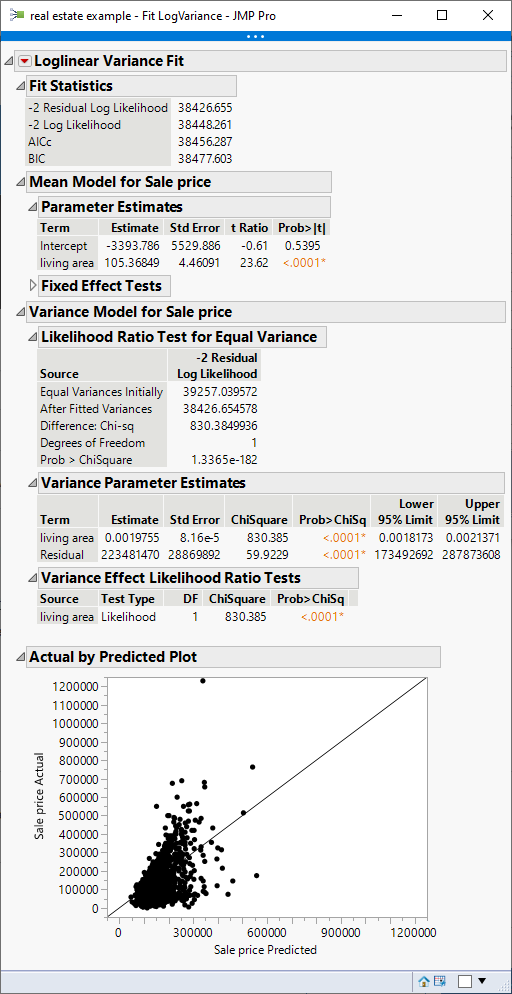
The second technique is to use a method that models the mean response and the response variance, and uses the variance function when regressing the mean. Change the fitting personality in the Fit Model launch dialog to Loglinear Variance and add living area as the effect for the second model. You are now fitting two models. One models the mean response and the other models the response variance. Both of them have living area as the sole predictor. The result is this:
The dependent variance is properly accounted for in this model. Of course, the residual pattern will still show that the variance is not constant. The only way to avoid that is to transform the response to stabilize the variance, but that should not be a goal in and of itself. You were just trying to handle the violation of assumption of constant variance in ordinary least squares regression.
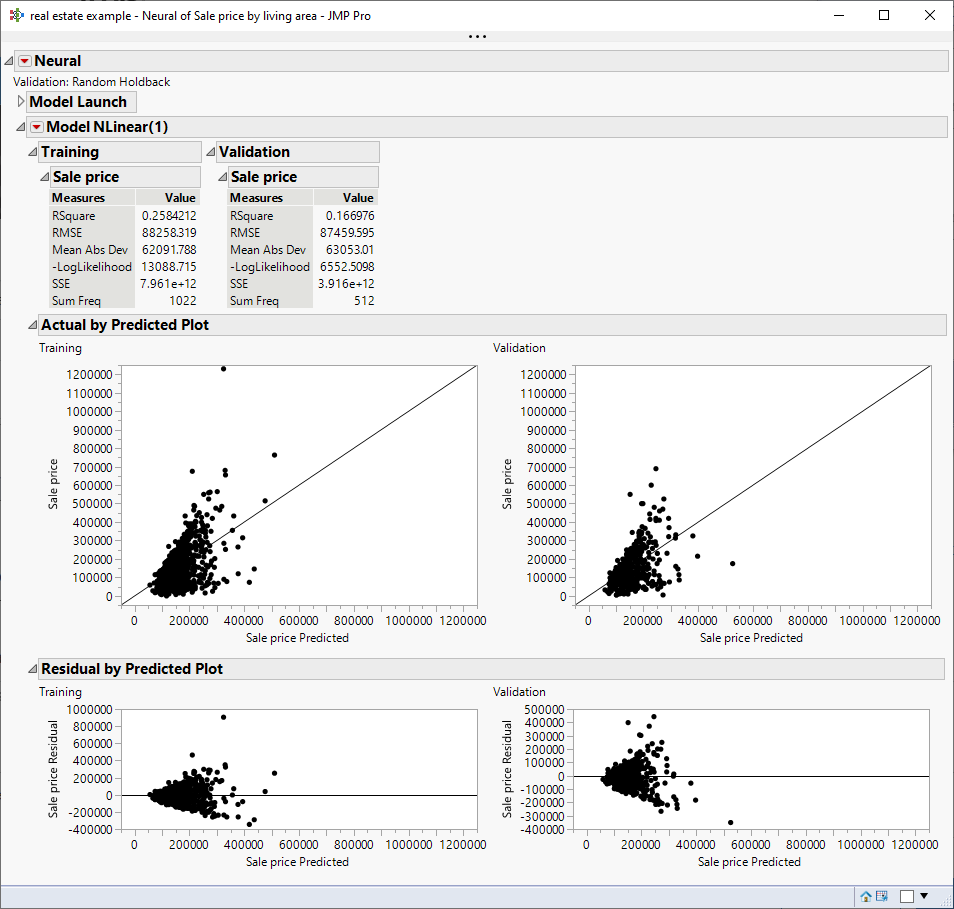
The third technique is to use another predictive model that does not assume constant variance. Here is the Neural model:
The residual pattern without transforming the response is the same as the unweighted linear regression, but the neural model estimation does not assume constant variance.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Weighted Least Squares and Residuals
The residuals are not the same with weighting as they are without weighting, but the overall pattern is the same. You fit a linear model in both cases and even though the two sets of parameter estimates are not identical, you are still plotting actual price minus predicted price versus predicted price. The weights affect the parameter estimates, not the pattern of residuals.
Weighting in this linear regression is by reciprocal variance, but the variance function might be difficult to determine in this case. So there are other techniques that can help. The first technique is to transform the response and therefore alter the variance. The Box-Cox transformation is used for several purposes, including stabilizing the response variance. The command is in the Factor Profiling sub-menu under the red triangle for Fit Least Squares. Here is the linear regression using the transformed response:
I didn't spend any time selecting the lambda parameter for the transformation, so you might do better with another value, but you can see that the residual pattern is different and getting closer to constant variance.
The second technique is to use a method that models the mean response and the response variance, and uses the variance function when regressing the mean. Change the fitting personality in the Fit Model launch dialog to Loglinear Variance and add living area as the effect for the second model. You are now fitting two models. One models the mean response and the other models the response variance. Both of them have living area as the sole predictor. The result is this:
The dependent variance is properly accounted for in this model. Of course, the residual pattern will still show that the variance is not constant. The only way to avoid that is to transform the response to stabilize the variance, but that should not be a goal in and of itself. You were just trying to handle the violation of assumption of constant variance in ordinary least squares regression.
The third technique is to use another predictive model that does not assume constant variance. Here is the Neural model:
The residual pattern without transforming the response is the same as the unweighted linear regression, but the neural model estimation does not assume constant variance.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Weighted Least Squares and Residuals
Recommended Articles
- © 2026 JMP Statistical Discovery LLC. All Rights Reserved.
- Terms of Use
- Privacy Statement
- Contact Us