- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Discussions
Solve problems, and share tips and tricks with other JMP users.- JMP User Community
- :
- Discussions
- :
- Using DOE result as a quantitative or qualitative prediction (based on effect su...
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Using DOE result as a quantitative or qualitative prediction (based on effect summary)
Hi all,
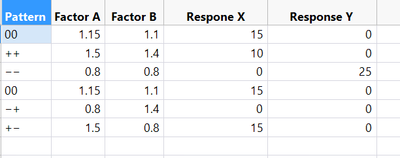
I'm doing a Full factorial DOE with 2 factors & 2 responses. & wondering how do
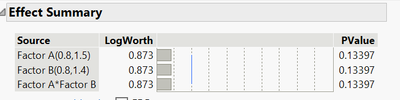
After testing & run the model. The result show that there is no significant factors & no significant model also.
But Looking at the interaction profiler. I see some clear trends in Factor A & response X.
So my question is how to use this result correctly.
- With this, I cannot predict quantitatively by using the regression model. Because it is statisticall insignificant (not practical)
- With the trend, I can still use that to predict it qualitatively (the trend) for ex: when increasing factor A, X will increase.
Am I understanding it correctly? or did I misinterpret this result?
Hope that some expert can help me. Thank you all
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Using DOE result as a quantitative or qualitative prediction (based on effect summary)
Hi @Justin_Bui,
There may be several explanations to why you don't find the terms in the model statistically significant :
- Too narrow factors ranges (so it may be more difficult to find statistical differences between high and low levels),
- High variability of the response(s),
- Inappropriate model (and/or choice of terms in the model),
- Too small sample size for the design (so low power for detecting statistically significant effects),
- Missing factor(s) explaining statistically the variation of the response(s),
- Effectively non-statistically significant factors,
- Combination of the options above,
- Other considerations...
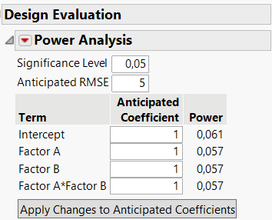
Considering your design and the assumed model, you can start evaluating you design to see how likely you would be to detect statistically significant effects if they are active (see script "Evaluate design" in the datatable). It seems you have quite low power for detecting main effects and interaction, so it's not a big surprise to not find any statistically significant terms for the response Y if you consider the high variability of this response (around 5% of chances to detect a statistically significant effect (if active) for a significance level of 0,05 and RMSE around 5 for the response Y with your 6 experiments) :
For a good starting point before modeling, it's always best to start simple, and do some graphs/visualizations to see the trends. That could further improve and inform your modeling options, and visualizations can also help you during the modeling to assess the relevance of your model (for example by looking at residuals plot, actual vs. predicted, etc...).
What is also interesting to consider is practical significance of the factor(s). In the example you provide for response Y and looking at the parameter estimates, does a variation of 20 in the response Y for one unit of factor B represents a practically significant increase/decrease ?
What you may find for response Y are trends, that could be further investigated by doing additional experiments (augmenting the design to add runs confirming this model, and/or replicating existing runs to better assess variability of the responses). The statistical significance helps you have more certainty in the interpretation of your results. For example in response Y, you can see that parameter estimates have relatively high standard error, meaning that the size of the effect may not be precisely estimated. So it's always best in those situations to interpret the trends with high caution.
For response X, it seems that a model involving the terms Factor A and its quadratic effect is sufficient to have an appropriate (or at least relevant enough) model. I let you assess the model for Response X in the datatable attached.
I hope this first answer may help you,
"It is not unusual for a well-designed experiment to analyze itself" (Box, Hunter and Hunter)
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Using DOE result as a quantitative or qualitative prediction (based on effect summary)
Justin,
A small "other consideration" to add on to the very well-articulated points raised by Victor_G...
In looking at the raw data, the values for Response X and Response Y seem to have very coarse measurements. While this may be an artifact of the translation of your example for posting- it points to a concern.
Across the six runs, X has only three options of values, and Y has only two. While it is nice that the repeats for factor pattern 00 came out the same, the lack of precision in the measurement system may impair process understanding.
*Consider if the measurement system precision can be improved*.
It will be difficult to build a useful mathematical model if the assay for response X can only report none(0), medium(10), large(15) and response Y is none(0) or some(25)...
Depending where burden of cost and time occurs in the DOE process, think about repeated measurements vs repeated runs.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Using DOE result as a quantitative or qualitative prediction (based on effect summary)
While Greg makes a good point, the issue is discrimination or effective resolution, not precision.
Recommended Articles
- © 2026 JMP Statistical Discovery LLC. All Rights Reserved.
- Terms of Use
- Privacy Statement
- Contact Us