- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Discussions
Solve problems, and share tips and tricks with other JMP users.- JMP User Community
- :
- Discussions
- :
- Re: Unequal Variance Violation
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Unequal Variance Violation
Hello,
I have tried to search in past discussion if there's something similar to my case. I don't find any.
I have a simple fictional data created to illustrate the scenario with data file attached.
Let's say there is:
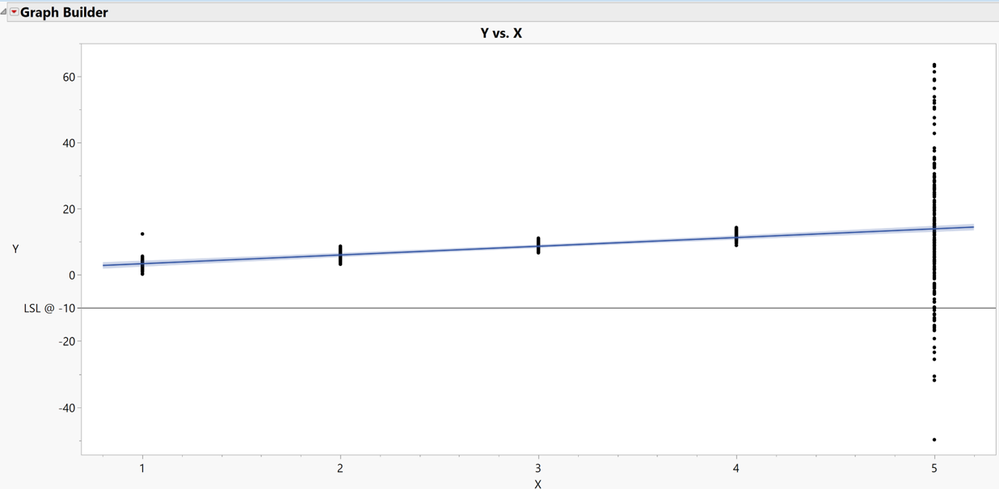
1 Factor (X) with level 1, 2, 3, 4, 5
1 Response (Y) with a Lower Spec Limit of -10
If we do a simple regression and come out with the model, the Profiler in this case will set the max desirability at X =5.
However based on a simple illustration, the worst setting would be at X=5 due larger variation of Y (some even failed the specs requirement). The best X should be set at 4.
Obviously we have a violation of the Unequal Variance assumption here.
We can try the Box-Cox Transformation on the Y in attempt to fix the Unequal Variance issue, or even try the Weighted Least Square.
However both of these methods mostly will not work, and in this case it doesn't work.
I know this seems like an extreme case, but for case study purposes, do we have any options where we have to live with the Unequal Variance issue and still we can get the "correct" maximized desirability?
Alternatively, we could utilize the Monte Carlo simulation to input a random noise to the Response and simulate the defect rate across X design space. However, Monte Carlo only allow to input one Stdev (noise) value and apply this across the whole prediction model.
So again, this method only works if the Unequal Variance is not violated.
How do we proceed with this?
Will an option to allow Monte Carlo to use the correct response noise per level in X (based on observed data) to perform the simulation, then this would have helped in identifying the correct setting for X.
For simplicity, let's say the Response Stdev is 1 when X= 1, 2, 3, 4 , and Response Stdev=19 when X=5.
So when we do Monte Carlo simulation, it will use the Stdev respective to the X level.
For sure, we do not have information on Response Stdev on other value of X, but at least have an option to perform this based on available data.
I have tried multiple options in the Monte Carlo noise features (weighted random noise, random noise by model....etc). It is still applying one uniform noise (stdev) to entire model.
Thanks.
B.r,
Chris
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Unequal Variance Violation
Is X a continuous factor in the actual case? Is the real case as extreme as the mock-up you created for us? Is there an explanation of why the response variance would change so much as the level or setting of X changes? Is it a measurement issue? Is it a process or a physical issue?
Those questions are most important. After that, you might consider using the LogLinear Variance fitting personality available through the Fit Model launch dialog if you can explain or justify these issues.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Unequal Variance Violation
I don't do the type of analysis you are interested in, but I'd suggest you change X to a nominal variable and then investigate the options. You might also define a new Y variable, defect or ok (depending on whether Y is less than -10 or not), and see what kind of analysis you can do for that nominal Y variable vs the nominal X variable. I'm sure there are some standard analyses that are appropriate for such situations, but it just seems like treating X as a continuous variable is not a good place to start.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Unequal Variance Violation
Is X a continuous factor in the actual case? Is the real case as extreme as the mock-up you created for us? Is there an explanation of why the response variance would change so much as the level or setting of X changes? Is it a measurement issue? Is it a process or a physical issue?
Those questions are most important. After that, you might consider using the LogLinear Variance fitting personality available through the Fit Model launch dialog if you can explain or justify these issues.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Unequal Variance Violation
Thanks Mark. Seems to be what I am looking for. To be tested of course.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Unequal Variance Violation
Any update?
Recommended Articles
- © 2026 JMP Statistical Discovery LLC. All Rights Reserved.
- Terms of Use
- Privacy Statement
- Contact Us