- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Discussions
Solve problems, and share tips and tricks with other JMP users.- JMP User Community
- :
- Discussions
- :
- using jmp to compare slopes and intercepts of multiple linear fits
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
using jmp to compare slopes and intercepts of multiple linear fits
Hi,
I need to compare the slopes and intercepts of 4 lines (linear regression y=ax+b) using jmp to see if any of them are similar or if they are significantly different from each other. Can anyone direct me towards a tutorial or a help document indicating the steps of how to do this. I am assuming I need to do an ancova test but have no clue how to setup the problem in jmp or if this is even the right test to do.
Any help will be highly appreciated.
Thanks!
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: using jmp to compare slopes and intercepts of multiple linear fits
Hi kaoutaraboucherif@gmail.com,
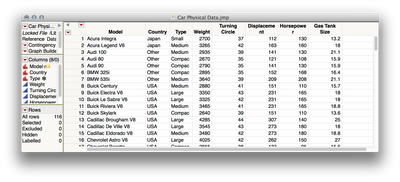
It sounds like a indicator-variable regression with an interaction is what you're looking for (an ANCOVA, by definition, does not have the interaction term allowing for independent slopes -- one of the most critical assumptions of an ANCOVA is homogeneity of regression). To set this up in JMP, you will need three columns: 1) a nominal column identifying the different groups; 2) a continuous column with the predictor; and 3) a continuous column with the response. I'll use Car Physical Data from the sample data directory for this example:
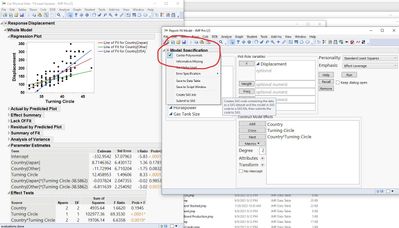
Suppose we want to know whether the relationship between Turning Circle and Displacement is the same for the cars made in different countries (USA, Japan, Other). Our model thus has three sources: a source for the effect of country (a test of the mean response by country), a source for the omnibus regression between turning circle and displacement (average relationship, ignoring country), and a source for the interaction (the degree to which each country's relationship of turning circle and displacement deviates from the grand regression). We'll use Analyze > Fit Model to define this model.
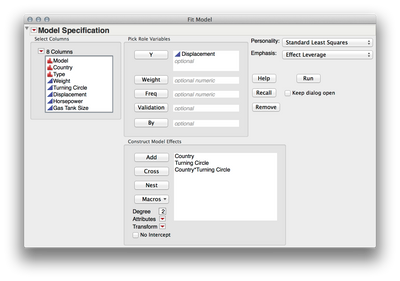
- To set this up, I did the following:
- Enter Displacement into the Y role.
- Select BOTH Turning circle, and country in the column list
- Click the "Macro" button and select "Full Factorial" - Notice this creates the three sources we need
- Press Run
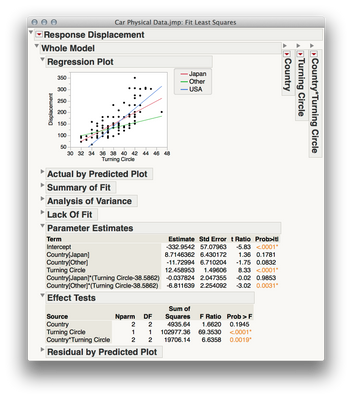
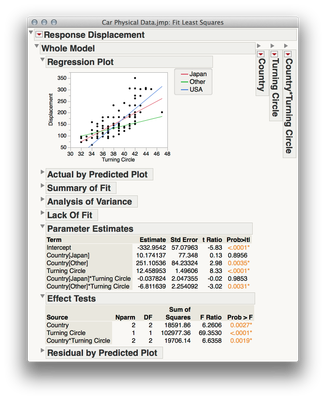
This yields the output above. Of most interest will probably the be the Parameter Estimates, and Effect Tests sections. If we look in the Effect Tests section under the interaction (Country*Turning Circle) we can see we have rejected the null hypothesis that the slopes are the same in each country -- e.g. we have evidence the regression of displacement on turning circle differs between the countries. Under the effect of Country we see we have not rejected the null hypothesis -- we do not have evidence that the MEAN displacement by country differs. If we really want a test of whether the intercepts of the models differ by country we need to uncheck "Center Polynomials" in the Fit Model specification under the Red Triangle. If we do that, we get the following output:
Notice that the source for the interaction is unchanged, as is the source for the omnibus regression, however the test of "Country" in this model is now a test for whether the mean response for country differs at 0 (i.e. the intercepts for each line), rather than a test for whether displacement differs by country at the mean of turning circle.
I hope this helps!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: using jmp to compare slopes and intercepts of multiple linear fits
Hi kaoutaraboucherif@gmail.com,
It sounds like a indicator-variable regression with an interaction is what you're looking for (an ANCOVA, by definition, does not have the interaction term allowing for independent slopes -- one of the most critical assumptions of an ANCOVA is homogeneity of regression). To set this up in JMP, you will need three columns: 1) a nominal column identifying the different groups; 2) a continuous column with the predictor; and 3) a continuous column with the response. I'll use Car Physical Data from the sample data directory for this example:
Suppose we want to know whether the relationship between Turning Circle and Displacement is the same for the cars made in different countries (USA, Japan, Other). Our model thus has three sources: a source for the effect of country (a test of the mean response by country), a source for the omnibus regression between turning circle and displacement (average relationship, ignoring country), and a source for the interaction (the degree to which each country's relationship of turning circle and displacement deviates from the grand regression). We'll use Analyze > Fit Model to define this model.
- To set this up, I did the following:
- Enter Displacement into the Y role.
- Select BOTH Turning circle, and country in the column list
- Click the "Macro" button and select "Full Factorial" - Notice this creates the three sources we need
- Press Run
This yields the output above. Of most interest will probably the be the Parameter Estimates, and Effect Tests sections. If we look in the Effect Tests section under the interaction (Country*Turning Circle) we can see we have rejected the null hypothesis that the slopes are the same in each country -- e.g. we have evidence the regression of displacement on turning circle differs between the countries. Under the effect of Country we see we have not rejected the null hypothesis -- we do not have evidence that the MEAN displacement by country differs. If we really want a test of whether the intercepts of the models differ by country we need to uncheck "Center Polynomials" in the Fit Model specification under the Red Triangle. If we do that, we get the following output:
Notice that the source for the interaction is unchanged, as is the source for the omnibus regression, however the test of "Country" in this model is now a test for whether the mean response for country differs at 0 (i.e. the intercepts for each line), rather than a test for whether displacement differs by country at the mean of turning circle.
I hope this helps!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: using jmp to compare slopes and intercepts of multiple linear fits
Thank you for the helpful tutorial! Extending the example, now that we know that the slopes and intercepts are different, how can we identify which slopes and intercepts are different from each other by post-hoc testing?
Thanks for any help.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: using jmp to compare slopes and intercepts of multiple linear fits
Was this question regarding evaluating Post hoc pairwise comparisons (comparing multiple slopes and intercepts) ever answered for running an indicator-variable regression with interaction analysis? Thanks!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: using jmp to compare slopes and intercepts of multiple linear fits
hello Julian, thank you for your explanation for this case, it's very helpful for me!
One more question, I can't find "Center Polynomials" in the Fit Model specification under the Red Triangle. My JMP version is 16.1 (not professional version). Can you show more detail how to test intercepts of the models differ by country ? thank you!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: using jmp to compare slopes and intercepts of multiple linear fits
I can actually help with this one. You have to deselect Center Polynomials from the Model Specification window. See attached picture. Hope this helps!
Recommended Articles
- © 2026 JMP Statistical Discovery LLC. All Rights Reserved.
- Terms of Use
- Privacy Statement
- Contact Us