- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Discussions
Solve problems, and share tips and tricks with other JMP users.- JMP User Community
- :
- Discussions
- :
- Re: Understanding the "Change Generating Rules" tab of the factorial screening p...
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Understanding the "Change Generating Rules" tab of the factorial screening platform
Hi everybody,
I am setting up a factorial screening design and want to adjust the 2FI aliasing so it fits my anticipated interactions.
What I would like is to have [Perform dialysis]x[Centrifugation % of max] aliased with [Imidazol]x[Covered surface area]
My problem is I cant get my head around the logic of the "Change Generating Rule" tab during design generation.
I read the help topic but I am still lost.
How do I interpret that weird table. Everything I do feels random and half of the time I do end up with a block effect aliased with a main effect.
cheers ben
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Understanding the "Change Generating Rules" tab of the factorial screening platform
Hi @BenGengenbach,
I tried to generate a screening design with the aliase you specified.
If we "code" your factors (except block) with X1, X2, ..., that means you have this generator for the fractional factorial design : I = 1245.
However, the presence of the block is quite difficult to take into consideration, as we have to take care that it is not confounded with main effects or any other effects, which is a quite tricky task since the aliases are fixed here.
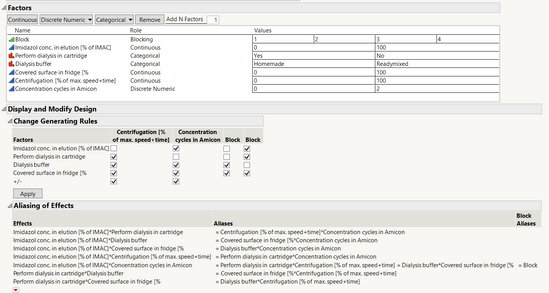
When trying to set up this generator in the generating rules, here is the configuration I have :
So here is an example of a design with the alias you defined (table attached):
DOE(
Screening Design,
{Add Response( Maximize, "Y", ., ., . ), Add Factor,
Add Factor( Continuous, 0, 100, "Imidazol conc.", 0 ),
Add Factor( Categorical, {"Yes", "No"}, "Perform dialysis in cartridge", 0 ),
Add Factor( Categorical, {"Homemade", "Readymixed"}, "Dialysis buffer", 0 ),
Add Factor( Continuous, 0, 100, "Covered surface in fridge", 0 ),
Add Factor( Continuous, 0, 100, "Centrifugation", 0 ),
Add Factor( Discrete Numeric, {0, 2}, "Concentration cycles", 0 ),
Set Random Seed( 1921021643 ), Make Design( 6 ),
Set Generators( [1 1 0 1, 1 1 0 1, 0 1 1 0, 1 0 1 0, 1 1 2 2, 0 0 0 0] ),
Simulate Responses( 0 ), Save X Matrix( 0 )}
)
But as suggested by @Mark_Bailey, I would also recommend a Custom Design, since you have different types of factors (categorical at 2-levels and continuous factors are accepted for DSD, but not the discrete numeric factor), it will be very easy to introduce a blocking factor if you have any constraints about the number of runs per day or any other blocking variable, and you can avoid having completely aliased effects in your design.
An example of a possible custom screening design with your factors could be :
DOE(
Custom Design,
{Add Response( Maximize, "Y", ., ., . ),
Add Factor( Continuous, 0, 100, "Imidazol conc.", 0 ),
Add Factor( Categorical, {"Yes", "No"}, "Perform dialysis in cartridge", 0 ),
Add Factor( Categorical, {"Homemade", "Readymixed"}, "Dialysis buffer", 0 ),
Add Factor( Continuous, 0, 100, "Covered surface in fridge", 0 ),
Add Factor( Continuous, 0, 100, "Centrifugation", 0 ),
Add Factor( Discrete Numeric, {0, 2}, "Concentration cycles", 0 ),
Add Factor( Blocking, 4, "Block" ), Set Random Seed( 2118942861 ),
Number of Starts( 1 ), Add Term( {1, 0} ), Add Term( {1, 1} ),
Add Term( {2, 1} ), Add Term( {3, 1} ), Add Term( {4, 1} ), Add Term( {5, 1} ),
Add Term( {6, 1} ), Add Term( {7, 1} ), Add Alias Term( {1, 1}, {2, 1} ),
Add Alias Term( {1, 1}, {3, 1} ), Add Alias Term( {1, 1}, {4, 1} ),
Add Alias Term( {1, 1}, {5, 1} ), Add Alias Term( {1, 1}, {6, 1} ),
Add Alias Term( {2, 1}, {3, 1} ), Add Alias Term( {2, 1}, {4, 1} ),
Add Alias Term( {2, 1}, {5, 1} ), Add Alias Term( {2, 1}, {6, 1} ),
Add Alias Term( {3, 1}, {4, 1} ), Add Alias Term( {3, 1}, {5, 1} ),
Add Alias Term( {3, 1}, {6, 1} ), Add Alias Term( {4, 1}, {5, 1} ),
Add Alias Term( {4, 1}, {6, 1} ), Add Alias Term( {5, 1}, {6, 1} ),
Set Sample Size( 16 ), Optimality Criterion( "Make A-Optimal Design" ),
"A-Optimality Parameter Weights"n( [1 1 1 1 1 1 1 1 1 1] ),
Simulate Responses( 0 ), Save X Matrix( 0 ), Make Design}
)
I hope this answer will help you,
"It is not unusual for a well-designed experiment to analyze itself" (Box, Hunter and Hunter)
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Understanding the "Change Generating Rules" tab of the factorial screening platform
Working with the generating rules is difficult for most people, even experts. It is difficult to assess the effect of a change in the rules.
Have you considered using a Custom Design or Definitive Screening Design instead of a fractional factorial? What is your reason for using a FF? Do you have constraints such as the number of runs? Do you have a model in mind?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Understanding the "Change Generating Rules" tab of the factorial screening platform
Hi Mark,
"It is difficult to assess the effect of a change in the rules." That is brilliant :D
Jokes aside, we want to do a quick screening and yes we are limited in the number of runs. Main effects are nice but there are some interactions that I would like to properly quantify and we do not have the luxury to go to a resolution V plan.
The workaround for my problem could be to check the aliasing in the current model and then simply swap the order of the factors during design generation.
At least that worked with DesignExpert software, however I thought the generating rules in JMP would be a bit more accessible.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Understanding the "Change Generating Rules" tab of the factorial screening platform
Hi @BenGengenbach,
I tried to generate a screening design with the aliase you specified.
If we "code" your factors (except block) with X1, X2, ..., that means you have this generator for the fractional factorial design : I = 1245.
However, the presence of the block is quite difficult to take into consideration, as we have to take care that it is not confounded with main effects or any other effects, which is a quite tricky task since the aliases are fixed here.
When trying to set up this generator in the generating rules, here is the configuration I have :
So here is an example of a design with the alias you defined (table attached):
DOE(
Screening Design,
{Add Response( Maximize, "Y", ., ., . ), Add Factor,
Add Factor( Continuous, 0, 100, "Imidazol conc.", 0 ),
Add Factor( Categorical, {"Yes", "No"}, "Perform dialysis in cartridge", 0 ),
Add Factor( Categorical, {"Homemade", "Readymixed"}, "Dialysis buffer", 0 ),
Add Factor( Continuous, 0, 100, "Covered surface in fridge", 0 ),
Add Factor( Continuous, 0, 100, "Centrifugation", 0 ),
Add Factor( Discrete Numeric, {0, 2}, "Concentration cycles", 0 ),
Set Random Seed( 1921021643 ), Make Design( 6 ),
Set Generators( [1 1 0 1, 1 1 0 1, 0 1 1 0, 1 0 1 0, 1 1 2 2, 0 0 0 0] ),
Simulate Responses( 0 ), Save X Matrix( 0 )}
)
But as suggested by @Mark_Bailey, I would also recommend a Custom Design, since you have different types of factors (categorical at 2-levels and continuous factors are accepted for DSD, but not the discrete numeric factor), it will be very easy to introduce a blocking factor if you have any constraints about the number of runs per day or any other blocking variable, and you can avoid having completely aliased effects in your design.
An example of a possible custom screening design with your factors could be :
DOE(
Custom Design,
{Add Response( Maximize, "Y", ., ., . ),
Add Factor( Continuous, 0, 100, "Imidazol conc.", 0 ),
Add Factor( Categorical, {"Yes", "No"}, "Perform dialysis in cartridge", 0 ),
Add Factor( Categorical, {"Homemade", "Readymixed"}, "Dialysis buffer", 0 ),
Add Factor( Continuous, 0, 100, "Covered surface in fridge", 0 ),
Add Factor( Continuous, 0, 100, "Centrifugation", 0 ),
Add Factor( Discrete Numeric, {0, 2}, "Concentration cycles", 0 ),
Add Factor( Blocking, 4, "Block" ), Set Random Seed( 2118942861 ),
Number of Starts( 1 ), Add Term( {1, 0} ), Add Term( {1, 1} ),
Add Term( {2, 1} ), Add Term( {3, 1} ), Add Term( {4, 1} ), Add Term( {5, 1} ),
Add Term( {6, 1} ), Add Term( {7, 1} ), Add Alias Term( {1, 1}, {2, 1} ),
Add Alias Term( {1, 1}, {3, 1} ), Add Alias Term( {1, 1}, {4, 1} ),
Add Alias Term( {1, 1}, {5, 1} ), Add Alias Term( {1, 1}, {6, 1} ),
Add Alias Term( {2, 1}, {3, 1} ), Add Alias Term( {2, 1}, {4, 1} ),
Add Alias Term( {2, 1}, {5, 1} ), Add Alias Term( {2, 1}, {6, 1} ),
Add Alias Term( {3, 1}, {4, 1} ), Add Alias Term( {3, 1}, {5, 1} ),
Add Alias Term( {3, 1}, {6, 1} ), Add Alias Term( {4, 1}, {5, 1} ),
Add Alias Term( {4, 1}, {6, 1} ), Add Alias Term( {5, 1}, {6, 1} ),
Set Sample Size( 16 ), Optimality Criterion( "Make A-Optimal Design" ),
"A-Optimality Parameter Weights"n( [1 1 1 1 1 1 1 1 1 1] ),
Simulate Responses( 0 ), Save X Matrix( 0 ), Make Design}
)
I hope this answer will help you,
"It is not unusual for a well-designed experiment to analyze itself" (Box, Hunter and Hunter)
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Understanding the "Change Generating Rules" tab of the factorial screening platform
Hi Victor,
wow that is great, thanks a lot!
Regarding the design set up: Did you enter the design generator deducted from my desired aliasing or did you modify it afterwards via the "generating rules" tab?
In case of the later it would be great if you could explain how to interpret it, as even @Mark_Bailey noted that is table is quite tricky to understand.
Nevertheless I think I'll go with the optimal design as suggested by both of you.
The rational behind this is simply that the aliasing is less harsh and more evenly distributed between multiple 2FI, correct?
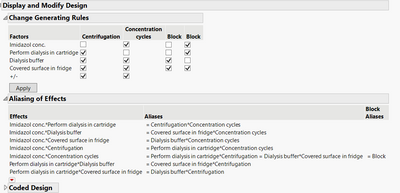
Left is the factorial right is the A-optimal:
And did you choose the A-optimality by default because I said screening?
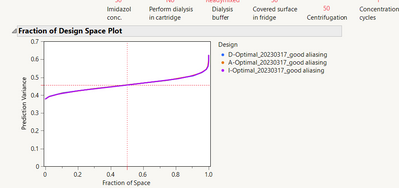
Interestingly when generating the optimal designs with the same factors, aliasing and, seeds, but different optimality criteria FDS is absolutely identical.
Is this to be expected?
regards ben
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Understanding the "Change Generating Rules" tab of the factorial screening platform
Hi @BenGengenbach,
I had to modify the "generating rules" tab in order to have the aliases you specified. This does take me some time to visualize the logic behind, and I'm (still) not 100% able to explain this logic, but as a general rule you have to check together the combinations you want to aliase, and avoid having the same pattern in different columns (to avoid aliasing main effects with block, or main effects with interactions). Each time you change a check, you can "apply" and visualize in the "Aliasing of Effects" panel if the aliases are correct depending on what you need or not.
Correct, an optimal design will try to "dilute" the aliases in a more uniform way than traditional fractional factorial designs, where aliases are simply present or absent ("binary aliases").
Traditionally, the optimality criterion for screening designs is D-optimality, as it enables to have a good precision on the estimation of coefficients : Optimality Criteria (jmp.com)
- D-optimality focuses on precise estimates of the effects.
- A-optimality results in minimizing the average variance of the parameters estimates of the model.
- I-optimality minimizes the average prediction variance over the design region, so it is better suited for Response Surface Models/predictive designs.
I would highly recommend to watch the presentation of Bradley Jones about modern screening designs, where he emphasizes on the advantages of A-optimal screening design vs. D-optimal screening design : 21st Century Screening Designs (2020-US-45MP-538) - JMP User Community
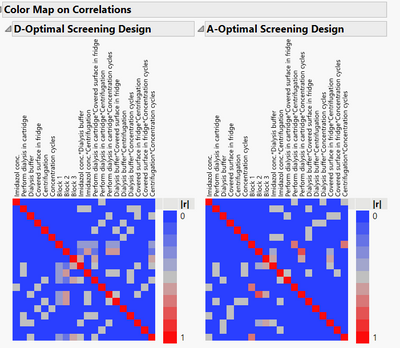
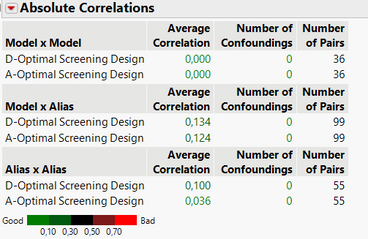
You can for example put different emphasis on the main effects you want to screen by specifying different weights, making A-optimal screening designs very flexible. As I didn't change the weights of the A-optimal design, the design is indeed very close from a D-optimal designs, except for correlations/aliases created in the designs :
And average correlations between designs :
Sorry for not being able to clarify much the "Generating Rules", I hope this answer will still help you a little more,
"It is not unusual for a well-designed experiment to analyze itself" (Box, Hunter and Hunter)
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Understanding the "Change Generating Rules" tab of the factorial screening platform
You might also consider adding higher-order terms and changing their estimability to "if possible." The idea here is that you are screening and want an economical design. You can reduce the minimum number of runs this way. The minimum number equals the number of terms whose estimability is 'necessary.' You want to add back 3-4 runs for every 'if possible' term you think might be active. For example, if I expected three interaction terms to be active but didn't know which ones, I would add three times 3 to 4 or 9-12 runs above the minimum.
Also, you can augment the original design after you complete your analysis if it indicates that some effects were missed the first time.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Understanding the "Change Generating Rules" tab of the factorial screening platform
The discrete numeric factor uses only two levels so it could be defined as a continuous or categorical factor. That change would allow a definitive screening design to be a candidate.
DOE(
Definitive Screening Design,
{Add Response( Maximize, "Y", ., ., . ), Add Factor( Blocking, 0, "Block" ),
Add Factor( Continuous, 0, 100, "Imidazol conc.", 0 ),
Add Factor( Categorical, {"Yes", "No"}, "Perform dialysis in cartridge", 0 ),
Add Factor( Categorical, {"Homemade", "Readymixed"}, "Dialysis buffer", 0 ),
Add Factor( Continuous, 0, 100, "Covered surface in fridge", 0 ),
Add Factor( Continuous, 0, 100, "Centrifugation", 0 ),
Add Factor( Categorical, {"0", "2"}, "Concentration cycles", 0 ),
Show Blocking Options( 1, 4 ), Number of Extra Runs( 4 ),
Set Random Seed( 2118942861 ), Make Design, Simulate Responses( 0 ),
Save X Matrix( 0 )}
);- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Understanding the "Change Generating Rules" tab of the factorial screening platform
I agree with your workaround @Mark_Bailey, but I see 2 potential problems/difficulties :
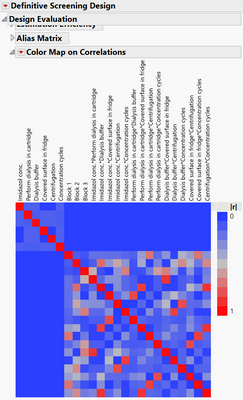
- If you specify concentration cycles as a categorical factor, you lose some of the property of DSD of having completely non-aliased main effects (unlike what you can obtain with A-optimal screening design with 16 runs):
So your parameters estimation for main effects is less precise that what you could obtain with the correct factor type in a Custom design, for 2 more runs : you may face a small increase in CI length, as well as a slightly higher standard error for estimates. And you won't be able to know what happens for 1 cycle, since categorical levels for this factor would only be 0 and 2.
- If using the factor as continuous, then DSD works fine and may not lose any of its nice properties, but if using the Prediction Profiler or any similar platform, the modeling won't be 100% accurate, as it can propose an optimum for any value between 0 and 2, without constraints, which is not the case in experiments. You can always round up the optimum value found, but why doing so many things to fit this special design when you have good alternative approaches ?
I'm generally in favor of DSDs, they are very nice designs with interesting properties, but I don't think "transforming" factors or the experimental space to fit a design is a nice idea (and quite contrary to the JMP philosophy "Fit a design to your problem, don't fit your problem to a design").
Best,
"It is not unusual for a well-designed experiment to analyze itself" (Box, Hunter and Hunter)
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Understanding the "Change Generating Rules" tab of the factorial screening platform
We are discussing the pros and cons of alternate designs. It would suffer if the last factor were defined as categorical with two fixed levels. Still, it offers more possibilities for estimating effects, albeit with reduced precision, than the main effect only regular fractional factorial design.
Recommended Articles
- © 2026 JMP Statistical Discovery LLC. All Rights Reserved.
- Terms of Use
- Privacy Statement
- Contact Us