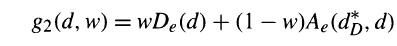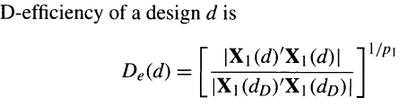- JMP will suspend normal business operations for our Winter Holiday beginning on Wednesday, Dec. 24, 2025, at 5:00 p.m. ET (2:00 p.m. ET for JMP Accounts Receivable).
Regular business hours will resume at 9:00 a.m. EST on Friday, Jan. 2, 2026. - We’re retiring the File Exchange at the end of this year. The JMP Marketplace is now your destination for add-ins and extensions.
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Discussions
Solve problems, and share tips and tricks with other JMP users.- JMP User Community
- :
- Discussions
- :
- Understanding the Alias-Optimal design algorithm, optimization of a fixed block ...
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Understanding the Alias-Optimal design algorithm, optimization of a fixed block effect
I was wondering: when one adds a fixed block effect to the alias-optimal design, how is it optimized?
For instance, following the explications by Jones and Nachtsheim(2011): is it optimized in the first objective being D-optimality optimization for the model terms, or, is it optimized in the secondary objective, being optimizing the orthogonality between Alias term and the model terms?
.. or something else?
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Understanding the Alias-Optimal design algorithm, optimization of a fixed block effect
The fixed effect of X5 (blocking factor) is in X1, not in X2.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Understanding the Alias-Optimal design algorithm, optimization of a fixed block effect
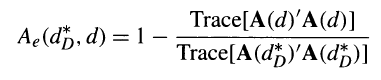
The algorithm is the same: coordinate exchange. The criterion is different. It is the minimum of the trace of A'A, where A is the alias matrix as described in the Help.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Understanding the Alias-Optimal design algorithm, optimization of a fixed block effect
Thank you Mark,
One point that remains confusing for me:
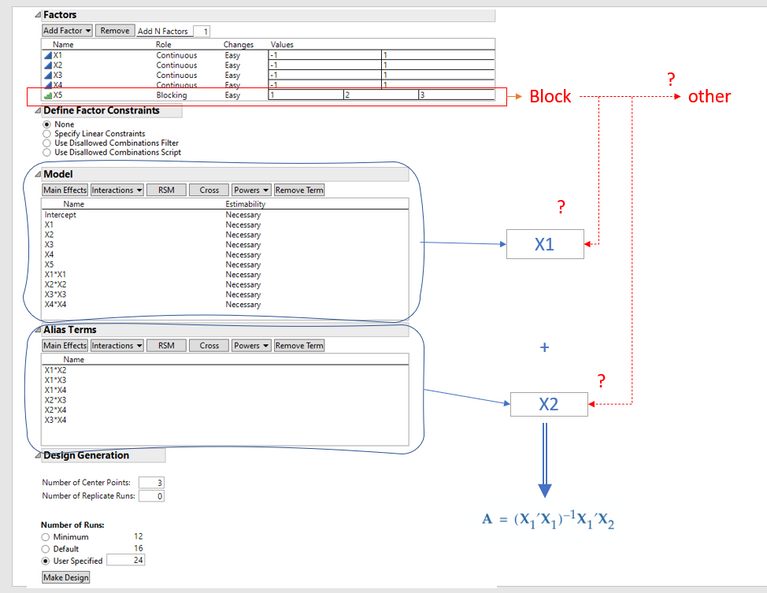
Is the Fixed Block effect placed in the Model (the X1) or in the matrix of model terms for the alias effects the (X2)?
See picture:
Reason for asking is that Following Jones and Nachtsheim (2011), i saw we minimize a mix of the trace of the Alias matrix and the D-efficiency with a weight factor to balance out. More formally, we minimize the objective function:
Where:
This let's me wonder:
If the block effect becomes a model term of design matrix X1 i guess it would optimize predictability (predictive variance) of the blocks as strongly as other model terms. If the block effect was in the model terms for matrix for the alias X2 we would optimize it's orthogonality against the X1 terms but it's predictive variance would be greater and estimated block effect sizes would not necessarily be orthogonal against potentially aliased effects.
Thank you for helping me understanding ;)
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Understanding the Alias-Optimal design algorithm, optimization of a fixed block effect
The fixed effect of X5 (blocking factor) is in X1, not in X2.
Recommended Articles
- © 2026 JMP Statistical Discovery LLC. All Rights Reserved.
- Terms of Use
- Privacy Statement
- Contact Us