- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Discussions
Solve problems, and share tips and tricks with other JMP users.- JMP User Community
- :
- Discussions
- :
- Time series forecasting with two correlated variables
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Time series forecasting with two correlated variables
I'm sure there is a way to do this either in Fit Model, Time Series Analysis, or Time Series Forecast. I have two time series grouped by age bracket. Columns are population and health care expenditure. I can do some forecast modeling no problem with the data individually. But, I have a population boom in the 40-60 year age bracket, so when they become the 70-80 year age bracket, they will cause an increase in the burden of health care which won't be captured if I just do the forecast on the expenditure column itself.
Thanks for any advice and happy new year to everyone out there!
Best,
Greg
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Time series forecasting with two correlated variables
A few clarifying questions and I'll offer some suggestions:
1. Are you trying to predict total expenditure for the group or per capita?
2. Do you have historical data for the x's and y's as group that ages from 40 - 60 to 70 to 80?
3. Are you trying to put together a predictive model or explanatory model?
And a modeling thought...with grouped x variables such as this while I don't dispute using Fit Model, or any of the time series modeling options might be valuable...I'm thinking one of the non linear modeling methods like Partition might be useful as well? I'm always a proponent of trying lots of apparently disparate modeling methods and seeing which one works best for the practical problem at hand.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Time series forecasting with two correlated variables
Thanks for respondiing!
(a) Total expenditure for the group is what I'm after (though per capita within each age bracket would be useful too)
(b) I have all the historical data - but what makes it a bit trickier is that at the younger adult ages, the burden on health care is rather flat across those brackets. But beyond 65-70, it increases rather exponentially. So when that spike in population hits that age bracket, the total expenditure will increase dramatically.
(c) Predictive - trying to estimate future costs to health care
With regards to non-linear - the historical data I have only goes back 20 years (so 20 rows), so I don't think my set is quite big enough to handle holding back data for validation for the non-linear models
Thank you!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Time series forecasting with two correlated variables
OK...here's my wacky ideas but hope that others will chime in. If I understand the nature of the data you've collected you can calculate on a per capita basis the expenditure of the age groups in the 'flat' part of the response...then watch each group advance through the years and calculate their per capita expenditures beyond 65 - 70...and if you are willing to extrapolate per capita expenditures for the baby boomer years, you can work your way up to total expenditures by multiplying per capita by estimated total population. If this makes any sense?
Obviously long range forecasting like this is fraught with unknowns. New advances/standards in care. A 'special cause' like COVID, or longer term population to population differences. For example...I'll wager that the percentage of people that were long time smokers in the over 70 age groups 20 years ago is much larger than it is today. Or heaven forbid the US government does something drastic like massive structural changes to social programs like Medicare which would very much influence what and who gets paid how much in the US health care system.
I always liked working on problems like this during my time in industry...I was part of a finance group at a former employer where we'd do long range forecasts for macro economic phenomena like employment, income, tax revenues, etc. If ever there was an area where George Box's famous quote, "All models are wrong...some are useful..." application areas such as this are the poster children.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Time series forecasting with two correlated variables
I am going to add one "wrong" model to what @P_Bartell has said.
There is a type of model in Time Series platform, known as the "Transfer Function Model". It models a response time series as a function of one or more input time series. In your example, "expenditure" seems like a response time series, and "population" seems like an input time series.
Check out these two resources that might be useful: documentation and a talk .
To me, it is not clear what you mean by "time series grouped by age bracket". Do you have multiple annual "expenditure" series for individual age groups. I.e. you have annual expenditure for 60 year age group, regardless the 59 old are moving int and 69 are moving out every year. So on so forth for 50 year age group, etc. And mean while, you have population count of 60 year age group every year. And the count are not on the same cohort, since 59 are moving in and 69 are moving out. If what I described is the case, you have quite a lot series.
Or maybe, your "expenditure" series is not broken up by age. Then you have one response series, and multiple input series. not one input series as you said. In this case, "Transfer Function Model" has multiple input series. In this setup, a Transfer Function Model can model the response at any time point as a weighted sum of current and/or previous inputs, and/or the past response.
After you have the model, then you need to forecast your input series and feed back into the model to forecast the response further into the future. And forecasting input series is a separate issue. In this case, forecasting population by age group is by itself a challenge. Age group distribution changed quite a bit in the past decades.
The last possible missing piece for this model is economic series as @P_Bartell mentioned. You may want to consider adding those series as additional inputs. E.g. inflation, macros, etc.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Time series forecasting with two correlated variables
Thank you both so much for all your suggestions and all the things I need to consider. To help clarify, I've uploaded the jmp table. And yes, there are so many factors to consider for the model - for the purpose of this exercise, I'm just trying to make it a "less worse" model. As I think about it, and maybe to help simplify things, the idea that Peng suggested as having one response series (in this case NL total which represents the total expenditures - all the columns before that split that figure out by age bracket). The following 20 columns or so are the population in age brackets and total). The columns after that are not really necessary. I guess to start my first question would be, after reading and watching the documentation and video above, what does the "Input List" in the launch window really mean and how does it differ from selecting "Transfer Function" from the red triangle dropdown menu, as I see when I just blindly put a column in ther "Input list", the output is entitled "Transfer function". I could not find an example of how "Input list" is used in any of the help or videos, though it does potentially seem applicable to this problem.
Thanks again!
Best,
Greg
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Time series forecasting with two correlated variables
Do you have JMP Pro? If so, you could likely use the Functional Data Explorer (FDE) to make models that could be used to make predictions. In the attached table, I stacked the data (only kept the N.L. and Population columns; didn't keep HC Expense and Canada columns). Screenshot below shows models for expenses fit to each of the age groups, using population as the Frequency for weighting. I'm not sure that's exactly what you're looking for, but there are many different ways to model in the FDE platform. Here's a link or two to relevant material on FDE.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Time series forecasting with two correlated variables
You data is intriguing. I will pick up a couple of things and talk in details.
First, Transfer Function Model. This is a rich class of models. And you may want to check out the bible on the subject Time Series Analysis, by George E. P. Box, Gwilym M. Jenkins, Gregory C. Reinsel. I will include an introductory version using a subset of your data; attached.
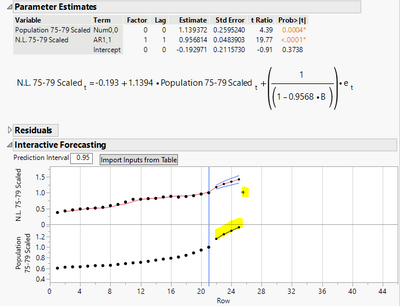
The subset is the 75-79 age group. It has an embedded script, which fit a bunch of Transfer Function Models. Run it. And you should see the following table. Use the check box to bring up the report one by one. And I am going to explain what they are. (BTW, I scaled the data. If I use the original data, the algorithm has trouble in some cases due to extreme values.)
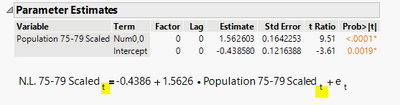
The first model, look at the formula picture. It says Scaled NL at time t is an intercept, plus a weighted value of Scaled Population at time t, plus an error. So this is just a simple linear regression. One can use Fit Y by X platform and get the same result.
But look at the residual plot below. It indicates, there are still unexplained patterns.
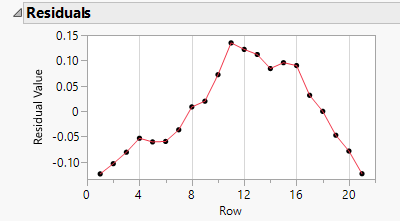
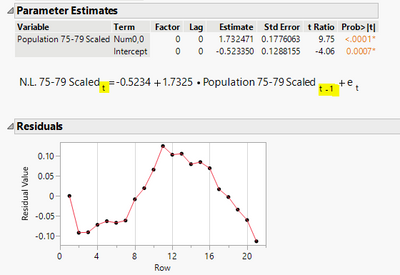
Now bring up the second model and look at the formula and residual.
The formula still looks like a regression. But the subscript on Scaled Population is t-1. This model says Scaled NL at time t is the sum of a constant, a weighted value of Scaled Population at the previous time t-1, and an error. So this model won't be easily fit in Fit Y by X without some data arrangement. Anyway, this is still not a good model, according to residual.
Now bring up the third model:
Its main part is the same as the first model, a simple regression, but the error term looks complicated. As you get familiar with the notation, you will recognize that the notation means: Scaled NL at time t involves it past value at time t-1. In summary, this model says: Scaled NL at time t is the sum of a constant, a weighted Scaled Population at time t, a weighted Scaled NL at time t-1, and an error term. So we are having more complicated models. And look at the residual plot, there are fewer obvious patterns.
The 4th model is similar, but used the lagged Scaled Population. The model says: Scaled NL at time t is the sum of a constant, a weighted Scaled Population at time t-1, a weighted Scaled NL at time t-1, and an error term.
The 5th and 6th models get more complicated, but unnecessary. But I leave them there to give you a sense how complicated things can go. And these examples are still considerably simple.
So as a summary, Transfer Function Model can be as simple as a simple linear regression, or more complicated by representing the response as a seemingly convoluted sum of historical values (and/or current for inputs) of response and input series values.
And seems there is at least one model fit the subset well. Let me use the third model. And look at the "Interactive Forecasting" part.
The highlighted markers are draggable. They should be self-explained if you move them. But to emphasize, the markers in the bottom frame represent future input series values. If you can forecast future input values, you should put the markers at desired places, and the output frame at top should show what the forecast on the response series looks like. Future input values can be imported in other ways, which I am not going elaborate (there is a button above the plot indicate its purpose for that.)
So the above is an example of using Transfer Function Model to analyze and forecast a subset of your data. But does not it make sense? To me, I am not sure. Your data is quite rick. The model fit this subset well. But it does not fit all subsets well. And I will leave that to you to conclude.
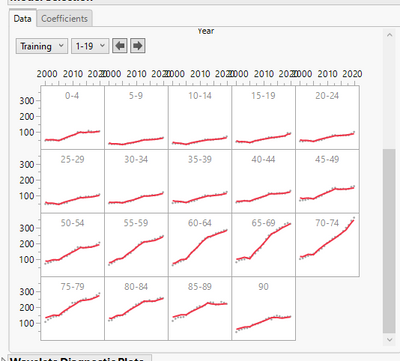
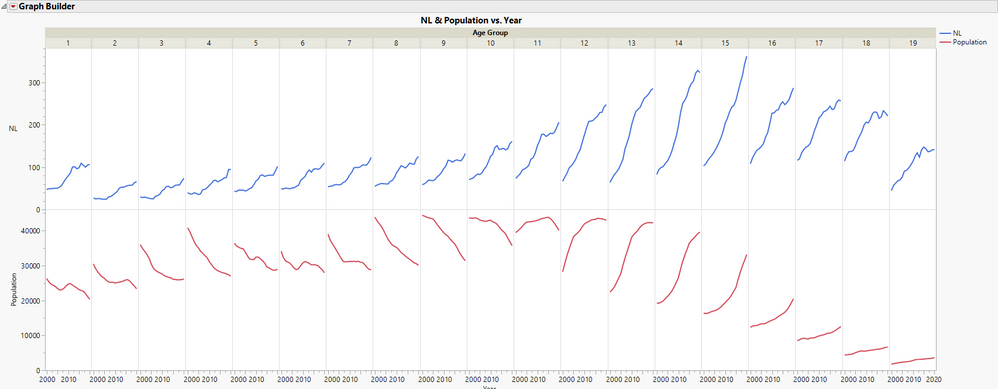
I did a plot to summarize what your data look like by age groups. The blue lines are NL series by age groups. And the red lines are corresponding Population series. All NL series have up tick trends. The Population series have downward trend for age groups younger than 50; and have upward trend for those older than 54. Several wonders:
- What this picture will look like next year, the year after, and so on?
- How to explain the cutoff at 50-54 group? And how to interpret the opposite trends between NL and Population for younger age groups, but same trends between them for older age groups.
- What do the wiggles at the end of NL series try to tell? They look interesting to me.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Time series forecasting with two correlated variables
The following looks at the data from a different angle.
On the top row, each frame is a plot of NL vs age groups, over years.
On the bottom row, each frame is a plot of Population vs age groups, over years.
To me, this plot provides more consistent perspectives about what is changing and what is not changing.
And if I look at the 21 frames on the top as a whole, and put them in a single frame consecutively, it reminds me of the famous airline passenger data, for which an seasonal ARIMA model is well known.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Time series forecasting with two correlated variables
Thank you again so much Peng. I'm starting to understand this much better but one thing is still confusing me. Using your uploaded file with the modified table, I am unable to reproduce your results unless I directly modify the script and run the script. I think the reason might be due to either a potential bug (which may have been resolved - I'm currently using JMP 15 but will be upgrading to 17 soon) or I am doing something quite stupid. But if you look at the attached screenshot, the top boxes are grayed out. And no matter what I do, I cannot enter a lag unless I change it directly in the script. Once again your help would be greatly appreciated.
Best regards,
Greg
Recommended Articles
- © 2026 JMP Statistical Discovery LLC. All Rights Reserved.
- Terms of Use
- Privacy Statement
- Contact Us