- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Discussions
Solve problems, and share tips and tricks with other JMP users.- JMP User Community
- :
- Discussions
- :
- Time Series Modelling: Concentrations
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Time Series Modelling: Concentrations
Hi all,
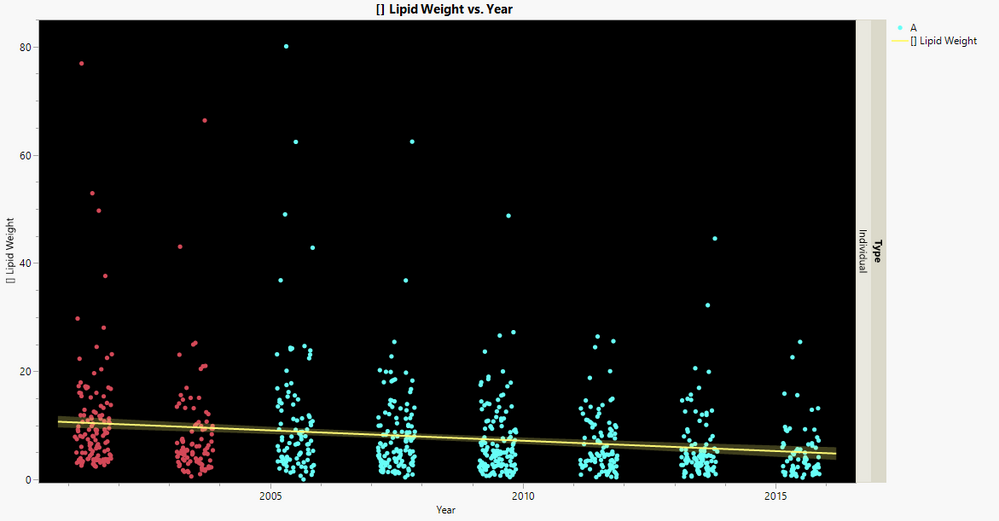
I'm looking to discuss the best modelling approach in JMP Pro 16 to predict time series concentrations of chemicals in individual samples extrapolated to today's date. Although the time series function in JMP will predict a spread of data illustrating the range at which the time series will fall under, I want to get more quantitative and predict what individual sample concentrations would look like. For instance, if we had 20 samples in 2021, what would their spread look like? Could I then further use these 20 samples to estimate a median/geometric mean of the concentration in 2021?
Or do I take a neural network approach where I predict the concentration of my multivariate chemical data based on date being the x factor? On attempt of this I get negative concentrations at times, which is not physically possible (but the model obviously doesn't know that). How to I constrain the data to predict realistic values based on the previous spread of data?
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Time Series Modelling: Concentrations
Not sure if this might work but since you are interested in spread...and running JMP Pro...maybe try out the quantile regression personality in the Generalized Regression platform? You could fit the 95% quantile for the spread or the 50% quantile for the median. Not sure it will help...but worth a try?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Time Series Modelling: Concentrations
Not sure if this might work but since you are interested in spread...and running JMP Pro...maybe try out the quantile regression personality in the Generalized Regression platform? You could fit the 95% quantile for the spread or the 50% quantile for the median. Not sure it will help...but worth a try?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Time Series Modelling: Concentrations
Along with what @P_Bartell suggested, you may want to log-transform you Y first before modeling, then inverse transform your prediction. That may address your negative prediction issue.
Other than that, there are other approaches to model "distribution changes over X". For example: Fit Life by X , Generalized Regression , among others.
Recommended Articles
- © 2026 JMP Statistical Discovery LLC. All Rights Reserved.
- Terms of Use
- Privacy Statement
- Contact Us