Testing for a difference in variance in a variable when there is a random effect

[#1]

Using "Fit Model" I'm predicting my dependent variable using a dichotomous nominal variable "Type" as well as a variable "Sample," which is a random effect (in JMP language that is; some would prefer to call "Sample" a random variable). This tests whether the two "Types" differ on my DV, again taking into account that "Sample" is a random effect. 

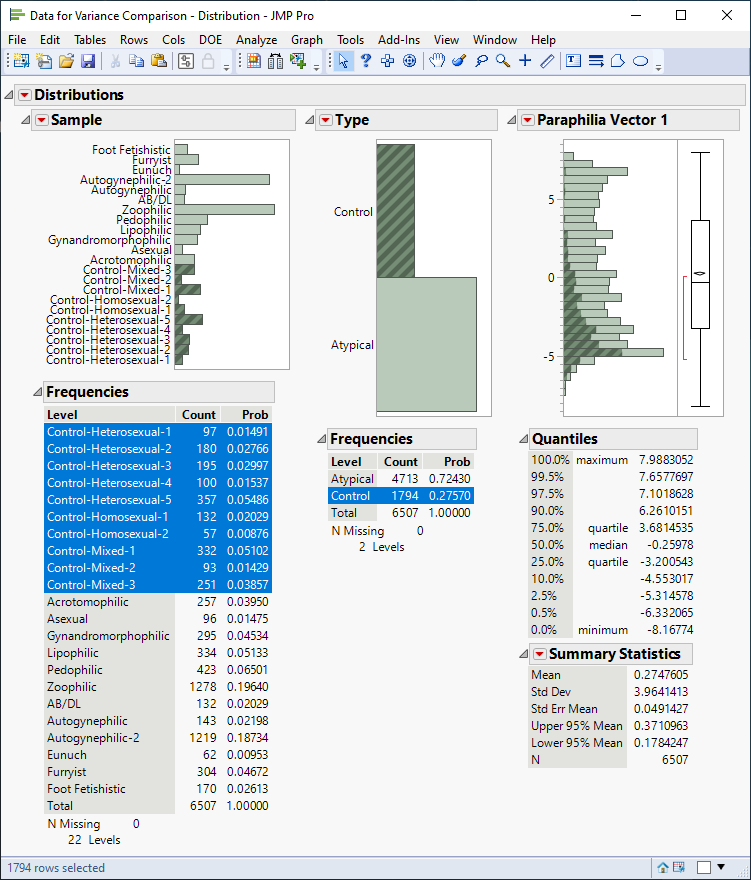
Interestingly, the sample means for one "Type" are much more spread out compared with the sample means for the other "Type." I can conduct a significance test on the difference in variances using an F test, if I am willing just to use the sample means. But this isn't quite kosher, because the sample means are estimated with error, and ideally, this should be taken into account. I can't figure out how to do this though. Perhaps "Mixed Models" has this ability. (I do have JMP Pro 16.) 

This is probably a bit "in the weeds" for this group, but if anyone has any ideas, I'd be grateful. I attach some data. DV=Paraphilia Vector 1, Type is the predictor of interest, and Sample is the random effect.

[#2]

I am not sure why you say Sample is a random variable. You assigned specific levels (classes) to each observation. The sample might be random, but the levels are not.

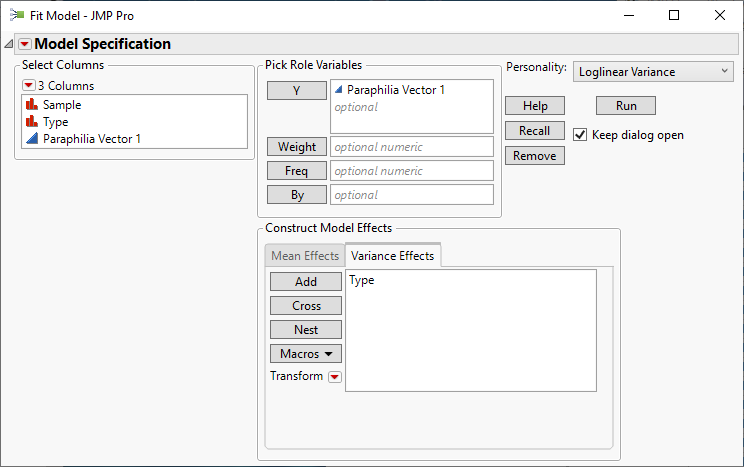
You might use Fit Model to define the model, and change the fitting personality to Loglinear Variance. Your data are not well-conditions for more than a simple main effects model. I assigned Sample as the location effect and Type as the spread effect. I could not include Type as a location effect because it is confounded with Sample. Including both variables as location effects.

But I can include Type as a spread effect to test your hypothesis.

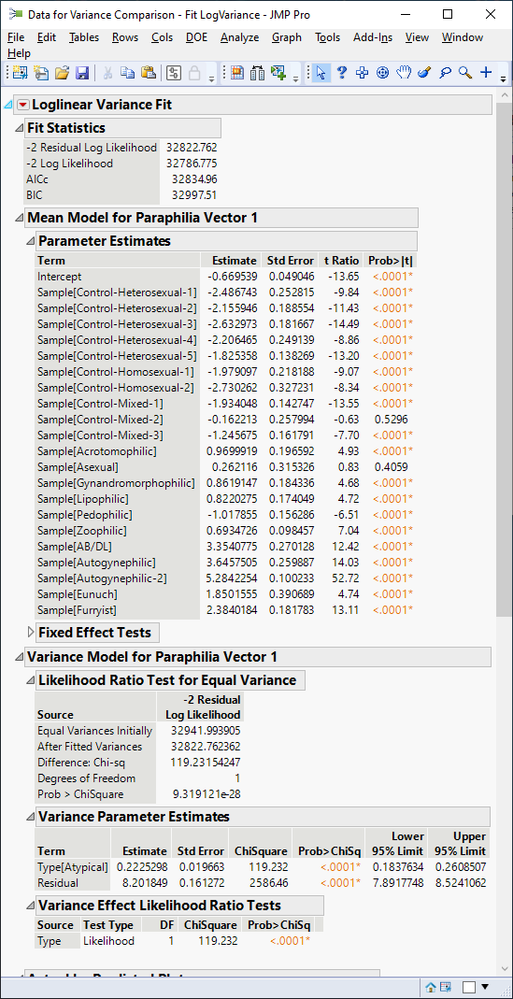
The estimated model from this specification exhibits no fundamental problems, but it might still be unsatisfactory.

It appears that the variance is significantly different for the two levels of Type.