- JMP will suspend normal business operations for our Winter Holiday beginning on Wednesday, Dec. 24, 2025, at 5:00 p.m. ET (2:00 p.m. ET for JMP Accounts Receivable).
Regular business hours will resume at 9:00 a.m. EST on Friday, Jan. 2, 2026. - We’re retiring the File Exchange at the end of this year. The JMP Marketplace is now your destination for add-ins and extensions.
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Discussions
Solve problems, and share tips and tricks with other JMP users.- JMP User Community
- :
- Discussions
- :
- Test For Curvature In 2 level full factorial with center points
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Test For Curvature In 2 level full factorial with center points
I am used to using Minitab for analyzing a 2 level factorial with some number of center points. In Minitab there is a test for curvature given (as opposed to a lack of fit test in JMP). Is there anything similar in JMP or should I just use the lack of fit test?
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Test For Curvature In 2 level full factorial with center points
Hello schuprj,
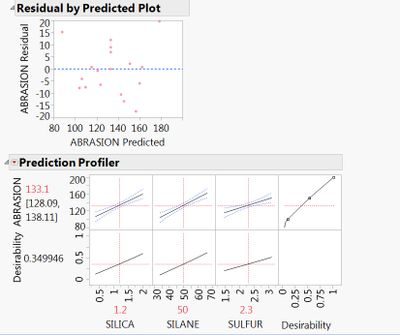
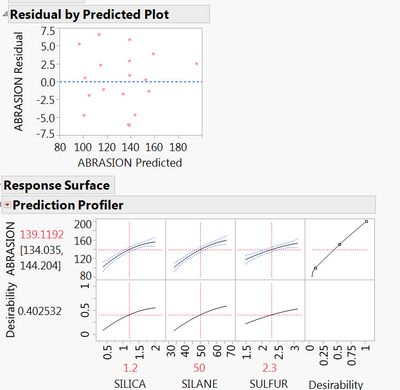
You have at least a couple of options for checking curvature. First is to plot the residual by predicted values under the red hot spot when you use Fit Model to build your model. Go to Row Diagnostics > Plot residual by predicted. Look at the scatter of the residual points and see if they are random or in some sort of pattern. Another option is to fit a main effects only model and then fit a response surface model. Two things will happen if there is curvature. Your fit model will improve if any of the quadratic terms are important to your model and you will see the curvature in your prediction profiler where the curvature terms are active.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Test For Curvature In 2 level full factorial with center points
Kind of a simple way to do a curvature test is to check if the model terms that would correspond to the presence of curvature are significant in the parameter estimates. If second order or quadratic terms aren't important you can't really have curvature.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Test For Curvature In 2 level full factorial with center points
Hello schuprj,
You have at least a couple of options for checking curvature. First is to plot the residual by predicted values under the red hot spot when you use Fit Model to build your model. Go to Row Diagnostics > Plot residual by predicted. Look at the scatter of the residual points and see if they are random or in some sort of pattern. Another option is to fit a main effects only model and then fit a response surface model. Two things will happen if there is curvature. Your fit model will improve if any of the quadratic terms are important to your model and you will see the curvature in your prediction profiler where the curvature terms are active.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Test For Curvature In 2 level full factorial with center points
Thanks for your quick post. As followup or clarification, a fairly
standard and simple test for curvature in this situation is to compare the
average of the center points to the average of the corner points. If this
difference is big enough then you probably have curvature and this warrants
further study to identify which factor(s). I can do this test manually in
JMP but thought that a fairly standard test like this would be displayable
somewhere in the dialogue. If not, so be it.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Test For Curvature In 2 level full factorial with center points
Kind of a simple way to do a curvature test is to check if the model terms that would correspond to the presence of curvature are significant in the parameter estimates. If second order or quadratic terms aren't important you can't really have curvature.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Test For Curvature In 2 level full factorial with center points
Hi schurpj,
Regarding to your lack of fit comment. Lack of fit - if significant - shows you there is something missing in the model which would improve the model significantly. This does not necessarily have to be a quadratic effect. it also could be a missing interaction effect or something you didn't measure but will have effect on your response.
"The difference between the error sum of squares from the model and the pure error sum of squares is called the lack of fit sum of squares. The lack of fit variation can be significantly greater than pure error variation if the model is not adequate. For example, you might have the wrong functional form for a predictor, or you might not have enough, or the correct, interaction effects in your model." (documentation)
Recommended Articles
- © 2026 JMP Statistical Discovery LLC. All Rights Reserved.
- Terms of Use
- Privacy Statement
- Contact Us