- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Discussions
Solve problems, and share tips and tricks with other JMP users.- JMP User Community
- :
- Discussions
- :
- Re: Tangent Line extrapolation from a known point on cuve
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Tangent Line extrapolation from a known point on cuve
Greetings,
Hope someone can help me resolve this calculation. I have hundreds of curves each being different. I calculated a critical point on each of the curves, from this point, I need to extrapolate perhaps using a tangent line to the horizontal axis and have that value recorded.
Regards,
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Tangent Line extrapolation from a known point on cuve
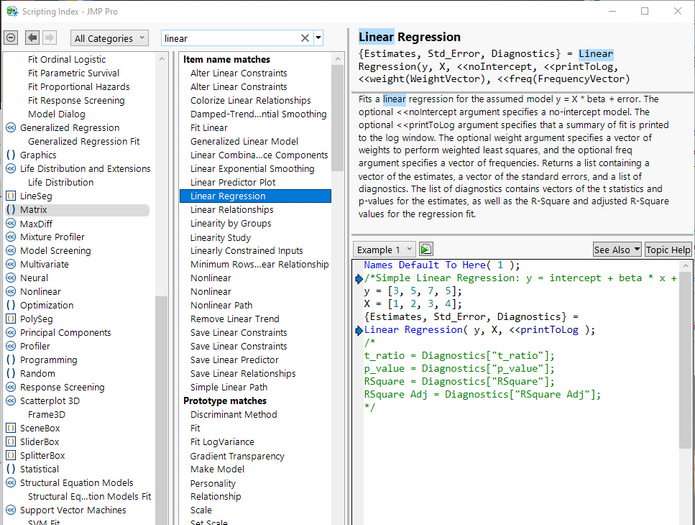
Using the JSL function called Linear Regression(), it should be easy to move the X and Y data that is right of the critical point, and to retrieve the intercept. Look into the Scripting Index for Linear Regression.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Tangent Line extrapolation from a known point on cuve
Take a look at the table script I put into a data table I made up for this problem.
You probably don't need the interactivity but it should give you an idea for solving the intercept based on a critical point selection.
The main solution in in the graph script:
selected_rows = Current Data Table() << Get Selected Rows();
If( N Items( selected_rows ) > 0,
Current Data Table() << Clear Row States();
critical_row = selected_rows[1, 0][1];
Current Data Table() << Select Rows( critical_row );
Current Data Table() << Colors( "Red" );
Current Data Table() << Clear Select();
);
Try(
x_prev = :X[critical_row - 1];
x_crit = :X[critical_row];
y_prev = :Y[critical_row - 1];
y_crit = :Y[critical_row];
slope = (y_crit - y_prev) / (x_crit - x_prev);
x_intercept = x_crit - y_crit / slope;
Y Function( slope * (a - x_intercept), a );
Marker( Marker State( 2 ), {x_intercept, 0} );
Text( {x_intercept, 0}, Eval Insert( " intercept = ^x_intercept^" ) );
);- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Tangent Line extrapolation from a known point on cuve
What kind of curves? What is their equation? What are the values for the parameters in the model equation? Can you use the derivative of the curve to calculate the tangent to the critical point? And is 'perhaps' a statement of your confidence in this approach?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Tangent Line extrapolation from a known point on cuve
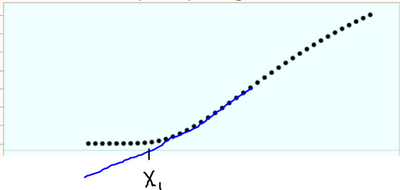
The curve will be similar to the picture below, the point where the blue line originates is the critical point for the tangent line to be extrapolated to horizontal axis.
Let me know if this makes sense
Thanks
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Tangent Line extrapolation from a known point on cuve
It looks like you are hunting for the linear portion of the curve and then estimating the x-intercept.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Tangent Line extrapolation from a known point on cuve
Hi
Yes, I have hundreds of these curves and all being different would be nice to automate those x-intercepts. I can probably calculate the linear slope using a point above and a point below in the array, then plot that line an record the value for the x-intercept...I'm just having a hard time conceptualizing that in JMP, I was able to do it VB but if JMP can do it will be much easier for the next set of evaluations.
Thanks
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Tangent Line extrapolation from a known point on cuve
Using the JSL function called Linear Regression(), it should be easy to move the X and Y data that is right of the critical point, and to retrieve the intercept. Look into the Scripting Index for Linear Regression.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Tangent Line extrapolation from a known point on cuve
thanks, I look into this further
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Tangent Line extrapolation from a known point on cuve
Take a look at the table script I put into a data table I made up for this problem.
You probably don't need the interactivity but it should give you an idea for solving the intercept based on a critical point selection.
The main solution in in the graph script:
selected_rows = Current Data Table() << Get Selected Rows();
If( N Items( selected_rows ) > 0,
Current Data Table() << Clear Row States();
critical_row = selected_rows[1, 0][1];
Current Data Table() << Select Rows( critical_row );
Current Data Table() << Colors( "Red" );
Current Data Table() << Clear Select();
);
Try(
x_prev = :X[critical_row - 1];
x_crit = :X[critical_row];
y_prev = :Y[critical_row - 1];
y_crit = :Y[critical_row];
slope = (y_crit - y_prev) / (x_crit - x_prev);
x_intercept = x_crit - y_crit / slope;
Y Function( slope * (a - x_intercept), a );
Marker( Marker State( 2 ), {x_intercept, 0} );
Text( {x_intercept, 0}, Eval Insert( " intercept = ^x_intercept^" ) );
);- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Tangent Line extrapolation from a known point on cuve
Hi
This is really elegant, it worked great for a single curve, I just need to figure out how to implement to multiple curves.
Regards,
Recommended Articles
- © 2026 JMP Statistical Discovery LLC. All Rights Reserved.
- Terms of Use
- Privacy Statement
- Contact Us