- RSS フィードを購読する
- トピックを新着としてマーク
- トピックを既読としてマーク
- このトピックを現在のユーザーにフロートします
- ブックマーク
- 購読
- ミュート
- 印刷用ページ
Discussions
Solve problems, and share tips and tricks with other JMP users.- JMP User Community
- :
- Discussions
- :
- Supress the effect of outliers when fitting the model and in predictions
- 新着としてマーク
- ブックマーク
- 購読
- ミュート
- RSS フィードを購読する
- ダイレクトリンクを取得
- 印刷
- 不適切なコンテンツを報告
Supress the effect of outliers when fitting the model and in predictions
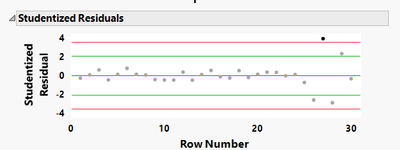
I assume that studentized residual is a good way to identify the ouliers.( Please correct me if i am wrong). And my question is how to filter out the the effect of these outliers in JMP prediction model? Will the model automatical avoid these outliers or should we delete them to get more accurate prediction ?
受理された解決策
- 新着としてマーク
- ブックマーク
- 購読
- ミュート
- RSS フィードを購読する
- ダイレクトリンクを取得
- 印刷
- 不適切なコンテンツを報告
Re: Supress the effect of outliers when fitting the model and in predictions
Hi @Mathej01,
Studentized residuals may be a good way to identify outliers based on an assumed model. See more infos about how the studentized residuals are calculated here : Row Diagnostics (jmp.com)
"Points that fall outside the red limits should be treated as probable outliers. Points that fall outside the green limits but within the red limits should be treated as possible outliers, but with less certainty." As you can see from the definition, there is no definitive certainty about the nature of outliers, and it may depends on the assumed model you imply.
I totally endorse and agree with the comment from @P_Bartell, there may be several explanations to the presence of your possible outlier (lurking variables, noise, different operators, ...).
The biggest advice to give about outliers before doing something about it could be : know your outliers. Depending on where they come from, what type they are (global, local/contextual or collective outliers) and the techniques to spot them, they are different, can be detected differently, and may have different influences on the models created :
- Global outliers : In univariate data, box-plots can easily detect them. In multivariate data, density-based clustering (DBSCAN, Optics, ...) or anomaly detection algorithms (Isolation Forest) might be helpful. They may result from recording/measurement errors, or anomaly samples.
- Contextual (conditional) outliers : Since outliers might not be outliers in all the dimensions of the data, K-Nearest Neighbors, Mahalanobis distances, Principal Components Analysis, Jackknife distances might be interesting to look at. These outliers are interesting to consider in the model, since their anormal values result from a specific context.
- Collective outliers : Clustering techniques might be helpful in this context : K-Means, Gaussian Mixtures, Hierarchical clustering, and other algorithms could be considered. They could be considered as a group.
A good advice is also to know if the possible outlier has an impact on the model, as all outliers are not (high)-leverage point. You can try to fit the same model in parallell with and without this point, to see if this outlier is (also) an high leverage point. Take a look at the plots Actual vs. Predicted, residuals plot, and metrics like RMSE PRESS and R² PRESS to better assess if the outlier has a any influence on the model.
Try to analyze what has caused some higher variability to the last 4-5 points (specific factor levels causing high noise, change of operator/measurement device, ... ?).
Hope this complementary answer will help you,
"It is not unusual for a well-designed experiment to analyze itself" (Box, Hunter and Hunter)
- 新着としてマーク
- ブックマーク
- 購読
- ミュート
- RSS フィードを購読する
- ダイレクトリンクを取得
- 印刷
- 不適切なコンテンツを報告
Re: Supress the effect of outliers when fitting the model and in predictions
Examining residuals can be a useful method for identifying 'outliers'. To answer the first half of your last question, "Will the model automatical (sic) avoid these outliers...", no.
Now let's back up a bit. Before excluding points from an analysis just to get a better fitting model may be akin to throwing the baby out with the bath water. Have you spent some time and energy examining root cause for these odd points? Does that investigation tell you something worthwhile knowing? And if your data shown in the plot is 'real', my eye says something happened in the system for the last 4 or 5 rows that was different from all the previous rows. Like if the row number is a production sequence, or maybe the run order of a designed experiment, some lurking nuisance factor entered the system and is causing these perturbations. Have you thought about this?
- 新着としてマーク
- ブックマーク
- 購読
- ミュート
- RSS フィードを購読する
- ダイレクトリンクを取得
- 印刷
- 不適切なコンテンツを報告
Re: Supress the effect of outliers when fitting the model and in predictions
Dear, Bartell,
Thank you so much for the answer. I think i should make a clarification here. The picture I sent with the question was just an example from my fitted model. And you are absolutely right, the last few data points are not just any ouliers or wrong data points. It was a DOE with different coatings done at different temperatures. And they were caused by some issue with caotingf at high temperature.
- 新着としてマーク
- ブックマーク
- 購読
- ミュート
- RSS フィードを購読する
- ダイレクトリンクを取得
- 印刷
- 不適切なコンテンツを報告
Re: Supress the effect of outliers when fitting the model and in predictions
Hi @Mathej01,
Studentized residuals may be a good way to identify outliers based on an assumed model. See more infos about how the studentized residuals are calculated here : Row Diagnostics (jmp.com)
"Points that fall outside the red limits should be treated as probable outliers. Points that fall outside the green limits but within the red limits should be treated as possible outliers, but with less certainty." As you can see from the definition, there is no definitive certainty about the nature of outliers, and it may depends on the assumed model you imply.
I totally endorse and agree with the comment from @P_Bartell, there may be several explanations to the presence of your possible outlier (lurking variables, noise, different operators, ...).
The biggest advice to give about outliers before doing something about it could be : know your outliers. Depending on where they come from, what type they are (global, local/contextual or collective outliers) and the techniques to spot them, they are different, can be detected differently, and may have different influences on the models created :
- Global outliers : In univariate data, box-plots can easily detect them. In multivariate data, density-based clustering (DBSCAN, Optics, ...) or anomaly detection algorithms (Isolation Forest) might be helpful. They may result from recording/measurement errors, or anomaly samples.
- Contextual (conditional) outliers : Since outliers might not be outliers in all the dimensions of the data, K-Nearest Neighbors, Mahalanobis distances, Principal Components Analysis, Jackknife distances might be interesting to look at. These outliers are interesting to consider in the model, since their anormal values result from a specific context.
- Collective outliers : Clustering techniques might be helpful in this context : K-Means, Gaussian Mixtures, Hierarchical clustering, and other algorithms could be considered. They could be considered as a group.
A good advice is also to know if the possible outlier has an impact on the model, as all outliers are not (high)-leverage point. You can try to fit the same model in parallell with and without this point, to see if this outlier is (also) an high leverage point. Take a look at the plots Actual vs. Predicted, residuals plot, and metrics like RMSE PRESS and R² PRESS to better assess if the outlier has a any influence on the model.
Try to analyze what has caused some higher variability to the last 4-5 points (specific factor levels causing high noise, change of operator/measurement device, ... ?).
Hope this complementary answer will help you,
"It is not unusual for a well-designed experiment to analyze itself" (Box, Hunter and Hunter)
- 新着としてマーク
- ブックマーク
- 購読
- ミュート
- RSS フィードを購読する
- ダイレクトリンクを取得
- 印刷
- 不適切なコンテンツを報告
Re: Supress the effect of outliers when fitting the model and in predictions
おすすめの記事
- © 2026 JMP Statistical Discovery LLC. All Rights Reserved.
- 利用規約
- 個人情報の取り扱いについて
- お問い合わせ