- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Stationariy time series
I have a time series (Occ (%ocupation) vs. time stamp cfr. Time series model in annex) where the autocorrelation function shows a slow decay indicating non-stationarity, however the ADF test all are negative indicating a statationary Occ time series. Which criterion is right? I get extremely good resuts with ARMA as well as ARIMA (diffeferenced) models. Can I assess a non differenced (4,2) ARMA model as reliable taking into account the slow decay autocorrelation function? Or is differencing necessary? Remark: only after two differencing operations ACF & PCF become similar indicating stationarity. Kind regards Frank
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Stationariy time series
In addition to my foregoing question I have a problem with the location of the saved prediction formula; I would expect it to be saved in the last column of my data sheet as is the case for other models. Here, in time series analysis the model is saved in a new "Untiteled" data sheet? Can this be adjusted?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Stationariy time series
https://en.wikipedia.org/wiki/Augmented_Dickey%E2%80%93Fuller_test states that "The augmented Dickey–Fuller (ADF) statistic, used in the test, is a negative number. The more negative it is, the stronger the rejection of the hypothesis that there is a unit root ..." The Zero Mean ADF is not significant but that is likely due to the daily cycles in your data.
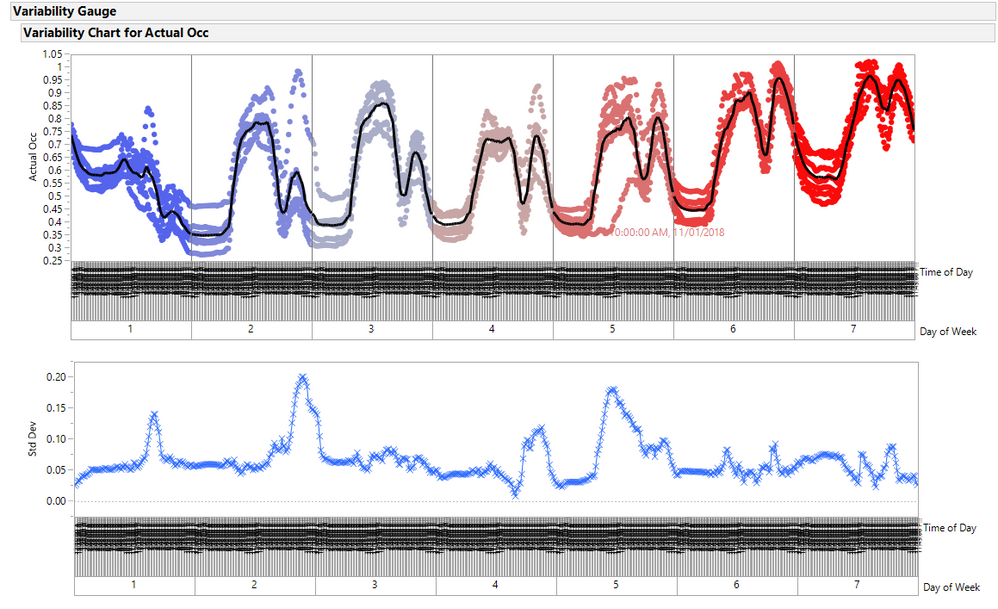
I added columns for Date, Day of Week and Time of Day. Below is a variability plot of OCC by Day of Week and Time of Day. The black line is the mean pattern for each day of the week. Note 11/01/2018 had an unusual pattern, (day after Halloween).
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Stationariy time series
Hello, thanks for your comment and effort to clarify avrage evolution, the unusual room occupation pattern indeed is halloween.
The goal of our study is to predict in next 15 - 60 minutes the room occupation level so we need to stay within the 15 minute lag intervals and try to construct a reliable time series model. You mention correctly that there are strong daily cycles so I assume that seasonal differencing is necessary? However doing so, even several times seasonality does not disappear, really confusing.. Even more surprising is that all models I checked - differenced or not - yield R² > 99%! Too good to be true, is there something fundamentally wrong in this analysis here?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Stationariy time series
I am sorry that I will not have time to propose a detailed solution. But hopefully this will provide a few leads:
- The daily pattern for Sunday is quite different from the the other days of the week, and Friday and Saturday have much higher usage.
- I would try creating a cycle by day and use a deviation model (cycles removed).
- I'd probably use an adjustable smooth, I have had good luck with Trigg & Leech methods that adjusts the lambda when the deviations are large, so that it can catch up.
Of course your RSquares will be larger that a real prediction since you are using all the data. You might want to take teh approach similar to control charts. You take an early period to create the baseline pattern, the model, then use, that model on the remaining period and the true RSquare will be based upon the residuals of actual - predicted for data not included in the model.
Finally, I would put a monitor, a control chart, to flag when the model is no longer predicting very well, especiall if you need a rapid response to escalating usage.
You shouls post which version of JMP, or JMP PRO and which OS. There are some new platforms and methods for this type of "process" that might be more useful than time series.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Stationariy time series
Hi, thanks a lot for your input. Fyi I am usig JMP 13.1version.
Indeed the daily patterns are different, do you mean that if the patterns were characteristic (like a fingerprint) for each day then one can, after differencing, create a predictive time series model for each? Unfortunately daily patterns may be disturbed by e.g. a holidyay so I think this will not always work?
I did several simulations with a testset (all new data) and my simple ARMA (4,2) model predictions work out fine for max.45 minutes, after that strong deviations start to show up although trends are kept.
I have an issue with the saved prediction formula: it is not saved in the last column of my original data sheet (as stated in the jmp tutorial) but in a new "untiteled" data sheet? Do you also encouter this? As for the prediction formula itself, what is the meaning of () - (number) What does that number mean? Can it be different from the number at the top in the equation? Regards, Frank