Specialized Modeling->Fit Curve Growth Rates

[#1]

Hello,

I am looking for a resource to explain how the growth rate parameters are calculated from the tangent at the inflection points, specifically for 3P and Weibull models. I need the ability to convert the growth rates back to biologically relevant numbers.

For example: If my Weibull growth rate is ~8, how do I convert this back to meters per day in reference to plant growth.
The growth rate should be a number closer to 0.06 meters per day.

Any help would be greatly appreciated.

-Steve

[#2]

I am not sure what you mean by 'how the growth rate parameters are calculated.' The parameters are estimated using variety of numerical methods depending on the platform default options or ones that you select. You can find the function of the curves by selecting Help > Books > Predictive and Specialized Modeling > Fit Curve > Statistical Details. For example, here you will find that the parameter called 'growth rate' by JMP is the power applied to ratio of X to the 'inflection point' in the case of the Weibull model:

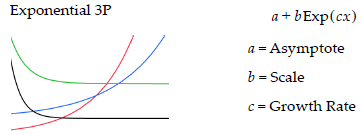
Here is the function for the 3P model you used:

I feel that I have missed your point, though. If you mean the instantaneous growth rate (change in Y with respect to change in X), then that would be the first derivative of this function with respect to the domain X. Because these functions are non-linear, the real growth rate will not be a constant.

Also, is time your X variable?

[#3]

@Mark_Bailey Thank you for the response.

Yes, I was trying to find the proper way to phrase my question.

I can now rephrase and ask how can the "growth rate" parameter be explained in biological context/importance?

Form your explination, it is not a growth rate in the sense of a slope? Saying that the growth rate unit of measure is meters/days would be incorrect?

My X variable is a time in days and my Y variable is the height in meters.

I would like to be able to define the maximum growth rate (meters/day) at the inflection point.

[#4]

No problem - I understand. It doesn't help that JMP developers had to come up with meaningful names for the function parameters when there are so many interpretations in different knowledge domains.

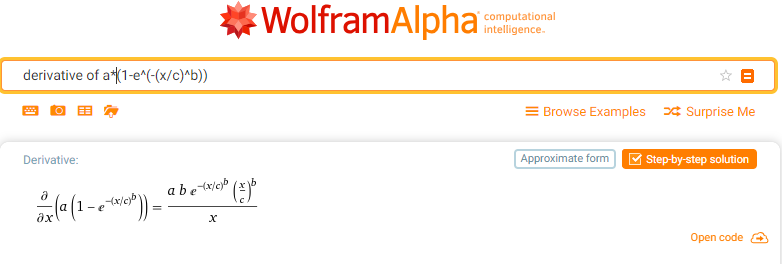
OK, you fit a model Y = f(X). We can use the estimated parameter values after differentiating the function: dY = f'(X). Here is the derivative for the Weibull model:

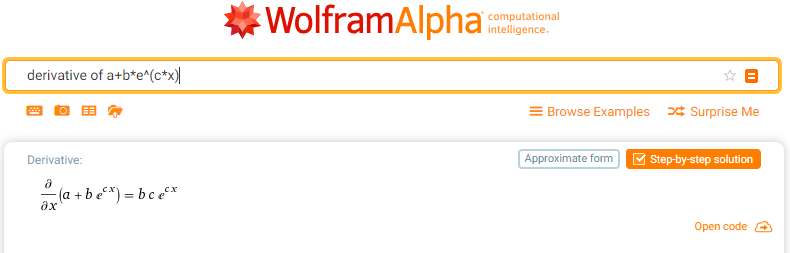
And here is the derivative for the Exponential 3P:

You can substitute the parameter estimates for the parameters and solve for 0 or plot these funtions versus X to see the maximum. (I don't think that the Exponential 3P has a maximum, though.)

[#5]

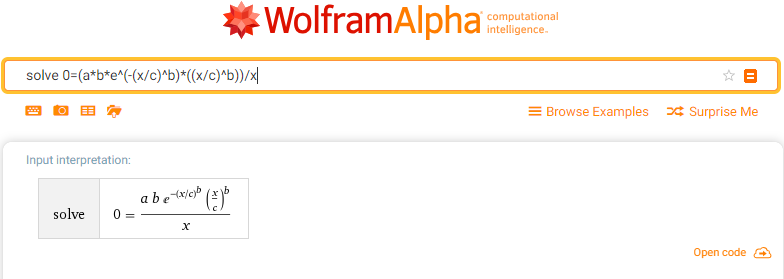
I think that if you replace the parameters in the derivative with the estimates from your Weibull fit in this request to solve the equation, you will get the X value (time) when it is maximum:

You can then substitute X into the derivative to get the corresponding maximum growth rate (change in y versus change in X).

An easier approach might be to create a new column (Rate) with a formula for the derivative with the estimates instead of the parameters and profile it. You can use the default desirability function (maximize) in the Prediction Profiler to find the corresponding rate and time.

[#6]

@Mark_Bailey 

Great thank you for the excellent explanation. This has helped a lot!

I have one final question, would the "growth rate" parameter of the JMP output have a unit of measure? Does it relate to the X or Y variable in terms of units (e.g. m/days) if I were to present it in a figure or table?

[#7]

I don't think so, but someone else might know otherwise.

I think that since Y = Weibull( X ), the parameter a (asymptotic plant height) has the unit meter and the parameter c (inflection point in time) has the unit day. It seem like the parameter b does not have any units. It is just a power, like a square or cube root.

[#8]

@Mark_Bailey 

Thank you again for your help.

I have a final question. Is there a publication that originally presents this form of the Weibull function?
I have seen several variants of the function and would like to reference the literature in which JMP used to develop their equation.

-Thanks

[#9]

There is much literature about this subject. I looked it up for you. See Help > Books > Reliability and Survival > References chapter:

Meeker, W. Q., and Escobar, L. A. (1998). Statistical Methods for Reliability Data. New York: John Wiley & Sons.

[#10]

For the 3P exponential growth model, if X has units of days, then the growth rate, c, would have units of (1/day).  You can think of it as the log linear rate per day.  (i.e.  Y=a+b*exp(c*x), so ln(Y-a) = ln(b) + c*x)