- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Discussions
Solve problems, and share tips and tricks with other JMP users.- JMP User Community
- :
- Discussions
- :
- Re: Smallest Covering Circle
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Smallest Covering Circle
I have a need to determine the smallest circle covering a group of 10 points (specifically the diameter of said circle). Does anyone have an idea of how I can calculate this in JSL?
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Smallest Covering Circle
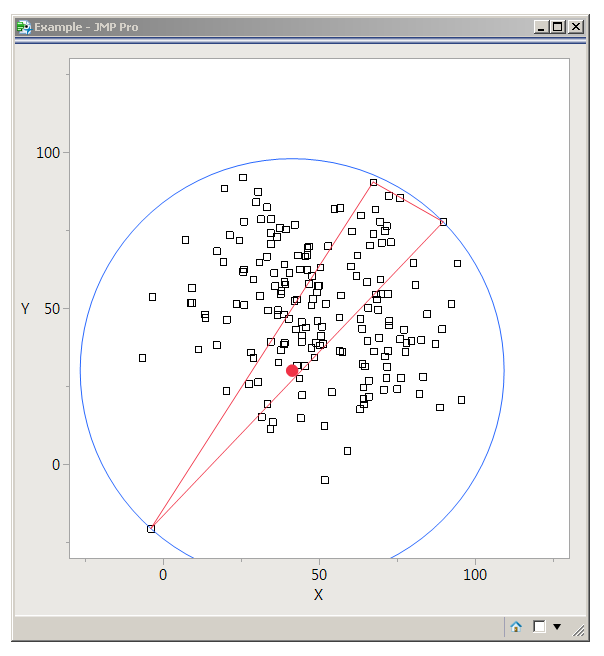
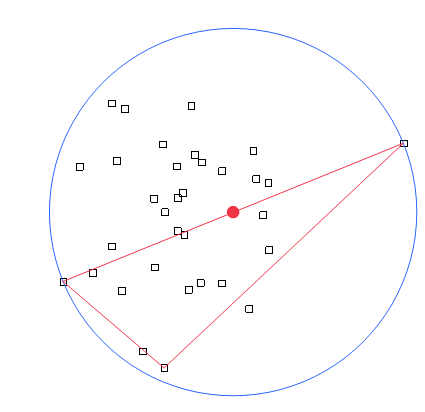
Don't know how to calculate an exact answer, but this seems to iterate to an approximation.
Update, 15feb2019 - this does not work well if there are only two points on the circle, see picture at end.
see slightly better JSL below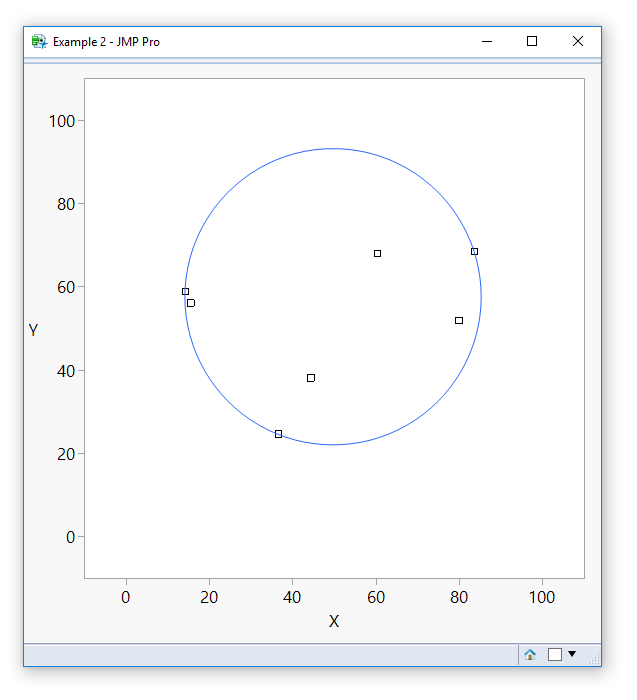
Here's the two point case that is not going to work well:
You could test for that and take the average of those two points when the third nearest point isn't at the radius, but that is getting clumsy and might have more issues. If you need an exact answer, you should look into the wikipedia answer. https://en.wikipedia.org/wiki/Smallest-circle_problem
might be hard... https://stackoverflow.com/questions/33443006/understanding-algorithm-for-finding-the-smallest-circle...
This is a little better, but the Welzl algorithm should give exact answers in less time:
points = J( 33, 2, Random normal( 50, 20 ) ); // make 33 random points
nrows = N Rows( points );
kdt = KDTable( points ); // make a nearest row look up table
center = Mean( points[0, 1] ) || Mean( points[0, 2] ); // pick a starting point
radius = 1e99; // make it big enough
fraction = .2; // fractional distance to move the center towards farthest point
For( i = 1, i < 1000, i++, // usually stops around 700
{indexes, distances} = kdt << knearestrows( nrows, center ); // just need farthest point, but get them all
farthest = indexes[nrows]; // last one is far away
howfar = distances[nrows];
If( howfar > radius, // if oscillating, make the fraction smaller
fraction = fraction * .9; // .5 stops the iterations too soon and gives really poor answers for 2-points on circle case
Show( i, fraction );
If( fraction < 1e-15, // good enough
Break()
);
);
radius = howfar;
// move slightly toward the farthest point
center = center + fraction * (points[farthest, 0] - center);
);
New Window( "Example",
Graph Box(
Frame Size( 500, 500 ),
X Scale( -30, 130 ),
Y Scale( -30, 130 ),
Marker( Marker State( 3 ), points[0, 2], points[0, 1] );
Pen Color( "Blue" );
Circle( {center[2], center[1]}, radius );
fill Color( "red" );
Pen Color( "red" );
Circle( {center[2], center[1]}, 2.0,"FILL" );
for(i=nrows,i>nrows-3,i--,
for(j=i,j>nrows-3,j--,
line({points[indexes[i],2],points[indexes[i],1]},{points[indexes[j],2],points[indexes[j],1]})
)
);
)
);
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Smallest Covering Circle
@kvnsngr ,
Are you referring to the smallest enclosing circle problem. If yes, do you have an algorithm in mind that you want to implement in JMP ?
Uday
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Smallest Covering Circle
Forgive me, I'm not very informed on the topic. But I found a paper by Sven Skyum that seemed to have an effcient algorithm.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Smallest Covering Circle
@kvnsngr ,
Well I really want to help you, however I would recommend and request that you try and at least come up with good pseudo code on what you would like the community to help with. If you could come up with a pseudo code, I or other community members can lead the way on how to achieve the pseudocode in JMP.
Uday
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Smallest Covering Circle
Don't know how to calculate an exact answer, but this seems to iterate to an approximation.
Update, 15feb2019 - this does not work well if there are only two points on the circle, see picture at end.
see slightly better JSL below
Here's the two point case that is not going to work well:

You could test for that and take the average of those two points when the third nearest point isn't at the radius, but that is getting clumsy and might have more issues. If you need an exact answer, you should look into the wikipedia answer. https://en.wikipedia.org/wiki/Smallest-circle_problem
might be hard... https://stackoverflow.com/questions/33443006/understanding-algorithm-for-finding-the-smallest-circle...
This is a little better, but the Welzl algorithm should give exact answers in less time:
points = J( 33, 2, Random normal( 50, 20 ) ); // make 33 random points
nrows = N Rows( points );
kdt = KDTable( points ); // make a nearest row look up table
center = Mean( points[0, 1] ) || Mean( points[0, 2] ); // pick a starting point
radius = 1e99; // make it big enough
fraction = .2; // fractional distance to move the center towards farthest point
For( i = 1, i < 1000, i++, // usually stops around 700
{indexes, distances} = kdt << knearestrows( nrows, center ); // just need farthest point, but get them all
farthest = indexes[nrows]; // last one is far away
howfar = distances[nrows];
If( howfar > radius, // if oscillating, make the fraction smaller
fraction = fraction * .9; // .5 stops the iterations too soon and gives really poor answers for 2-points on circle case
Show( i, fraction );
If( fraction < 1e-15, // good enough
Break()
);
);
radius = howfar;
// move slightly toward the farthest point
center = center + fraction * (points[farthest, 0] - center);
);
New Window( "Example",
Graph Box(
Frame Size( 500, 500 ),
X Scale( -30, 130 ),
Y Scale( -30, 130 ),
Marker( Marker State( 3 ), points[0, 2], points[0, 1] );
Pen Color( "Blue" );
Circle( {center[2], center[1]}, radius );
fill Color( "red" );
Pen Color( "red" );
Circle( {center[2], center[1]}, 2.0,"FILL" );
for(i=nrows,i>nrows-3,i--,
for(j=i,j>nrows-3,j--,
line({points[indexes[i],2],points[indexes[i],1]},{points[indexes[j],2],points[indexes[j],1]})
)
);
)
);
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Smallest Covering Circle
Best description I found: https://www.nayuki.io/page/smallest-enclosing-circle with implementations in several languages and a live demo on the page.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Smallest Covering Circle
Thanks a lot for the insight! I haven't fully implimented this yet but it seems like this might work for me.
Recommended Articles
- © 2026 JMP Statistical Discovery LLC. All Rights Reserved.
- Terms of Use
- Privacy Statement
- Contact Us
