- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Discussions
Solve problems, and share tips and tricks with other JMP users.- JMP User Community
- :
- Discussions
- :
- Re: Significant values in parameter estimates
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Significant values in parameter estimates
Hi all,
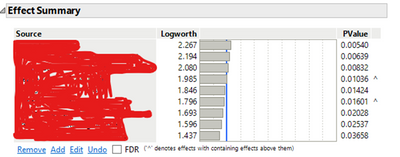
I have made a custom DOE and have been analysing my data first step-wise to identify important effects then standard least square to find significant effects. I could see the following significant effects:
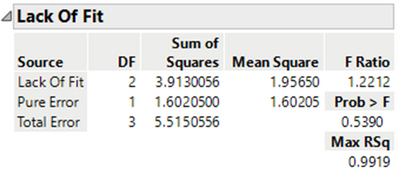
I then checked the Lack of fit, which was also ok
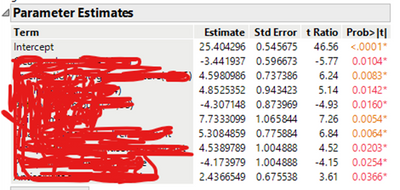
I then looked further down through the parameter estimates and saw a lot of red values for the parameter estimates. What does this mean for my model? Is it no longer significant even though effect summary and lack of fit says it is?
Many thanks for you help in answering this question.
Kind regards,
Hanna
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Significant values in parameter estimates
Hi,
The red highlight represents p-values below 0.05 and greater than 0.01
The orange highlight represents p-values below 0.01
All the parameters listed in the last table are significant.
Best,
TS
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Significant values in parameter estimates
It is known as 'conditional formatting.' You can find it by selecting File > Preferences (Windows) or JMP > Settings (Mac). Select the Reports group on the left.
You can turn this formatting on or off. You can modify the rules and formats. You can add your own formats.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Significant values in parameter estimates
My comments, without any understanding of your situation:
1. The reason you have so many significant factors is because you have very few DF's for estimating error. My guess is your experiment is underestimating the true error. You really need to know what is the basis of the tests before you interpret them.
2. Not sure why you are using stepwise for analysis of DOE? You should have a predicted model á prior. I really like the Daniel approach to analyzing experiments. He saturates the model and uses normal and half-normal plots to assess interesting effects. I would add Pareto plots to assess practical significance and, of course, Box would add Bayes plots. All of these plots are available in JMP (see Effect Screening).
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Significant values in parameter estimates
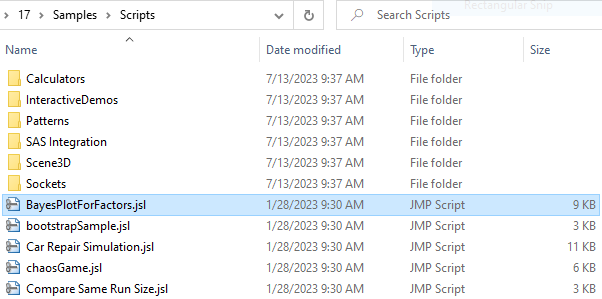
The Bayes Plot that @statman referred to is available in the Fit Least Squares platform. It implements the first version published by George Box, which only considered the main effects. Box later updated the method to include higher-order terms. We provide the updated plot as a JMP script in the Samples/Scripts folder here (Windows):
I also attached the script to my reply.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Significant values in parameter estimates
Oh yeah. Thanks for that script!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Significant values in parameter estimates
Hi @statman ,
thanks for the fast reply. The problem for us was a limitation in amounts of experiments we could perform. What we would usually do in that case is still check for 2nd factor interactions through the stepwise approach and only take those 2nd factor interactions into account that come out of the stepwise approach in addition to the 1st order interactions. Those we then model using standard least square effect screening in jmp. This works quite well if there is only a limited amount of effects being active. However here, as you mentioned this let to an overfit. Would your suggestion be to augment the design to add more experiments in to have more experiments to estimate the error? How would the augmentation have to be, just increase experiments or adding in 2nd order effects ahead of augmentation?
2. Could you elaborate on this and how to perform this in jmp? I am no statistician but chemist by training, so i might be missing some background regarding this answer.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Significant values in parameter estimates
I'm happy to share my thoughts, but I don't have a sufficient understanding of your situation to provide specific advice (Like should you augment, replicate or what), so I'll speak in generalities which naturally is an oversimplification:
What you are doing in an experiment is trying to compare the effects of terms in your predicted model (main effects, 2nd order linear, etc.) to random error (noise) and to each other. Since experiments are, by design, narrow inference space studies (you have essentially removed the time series and so the effects of noise that change over time are naturally excluded) you have to exaggerate the effects of noise to be representative of future conditions.
“Unfortunately, future experiments (future trials, tomorrow’s production) will be affected by environmental conditions (temperature, materials, people) different from those that affect this experiment…It is only by knowledge of the subject matter, possibly aided by further experiments to cover a wider range of conditions, that one may decide, with a risk of being wrong, whether the environmental conditions of the future will be near enough the same as those of today to permit use of results in hand.”
Dr. Deming
Unfortunately, as the experimental conditions become more representative of future conditions, the precision of detecting factor effects can be compromised. One of the strategies to improve precision lies in the level setting for your design factors (hence the advice in screening designs is to set levels bold, but reasonable). Strategies to handle noise are critical to running experiments that are actually useful in the future. There are a number of strategies to handle noise (e.g., RCBD, BIB, split-plots (for long-term noise) and repeats (for short-term noise). When you have significant resource constraints, your options are limited.
The bottom line is if you are using only statistical significance tests, the less representative your estimate of the random noise, the less useful the statistical test (it is less than useful to have something appear significant today and insignificant tomorrow). Stepwise uses statistical tests (of the data in-hand) and, again, if that data is not representative, those tests may be worse than useful (commit both alpha and beta errors). It is kind of interesting how there is a focus solely on the alpha error (p-values for example) in screening situations when, perhaps, the most dangerous error is the beta.
I'm not sure what you mean by "Could you elaborate on this and how to perform this in jmp?" Do you mean design appropriate experiments or perform appropriate analysis?
All analysis is dependent on how the data was acquired. For your analysis, since you have an unreplicated design, run Fit Model, assign ALL DF's to the model (saturate the model). Run Standard Least Squares personality. Once you have the output, select the red triangle next to each response and select Effect Screening. There you will find the options of Normal plot, Pareto plot and Bayes plot (see additional script above).
"Results of a well planned experiment are often evident using simple graphical analysis. However the world’s best statistical analysis cannot rescue a poorly planned experimental program."
Gerald Hahn
ps, you might enjoy reading Cuthbert Daniel as he never took a class in statistics, but is a profound experimenter.
Recommended Articles
- © 2026 JMP Statistical Discovery LLC. All Rights Reserved.
- Terms of Use
- Privacy Statement
- Contact Us