- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Discussions
Solve problems, and share tips and tricks with other JMP users.- JMP User Community
- :
- Discussions
- :
- Significance of factors in Definitive Screening Design
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Significance of factors in Definitive Screening Design
Dear JMP ommunity,
I have conduced a 37-run Definitive Screening Design for 15 factors to find the dominating ones. I have set the p-value as 0.05 and in the documentation it says that a factor will be shown as "active" if the p-value is lower than the defined threshold (i.e., 0.05). However, in some cases, when I fit the definitive screening design, there are factors with p-value of higher than 0.05 appearing as "active or significant". Below, I have attached an example of what I mean. Can someone help me to solve this ambiguity?
- Tags:
- windows
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Significance of factors in Definitive Screening Design
Hi @Ahmedhadi,
Welcome in the Community !
It is difficult to help you without looking at your design and without knowing how you design it.
Nevertheless, I think you may find answers in this Help section about the analysis of DSDs : Statistical Details for the Fit Definitive Screening Platform (jmp.com)
You might also be interested in the original publication of the Fit DSD method : Bradley Jones & Christopher J. Nachtsheim (2016): Effective Design-Based Model Selection for Definitive Screening Designs, Technometrics, DOI: 10.1080/00401706.2016.1234979
As you can see on the screenshot, the analysis of DSDs is done in 2 steps to take into account the specific structure of DSD :
- First stage involves main effects identification with the responses values
- Second stage involves 2-factors interactions and quadratic effects identification (based on Effects Heredity principle) with the responses residuals from the first stage model.
From the low amount of information provided, if your 37 runs DSDs involves 15 continuous factors, you may have 4 extra runs in your design, so in your stage 1, the variance from the supposed model (with all main effects) is estimated against error variance from the 4 extra runs. This enable to identify active effects below a certain p-value threshold (defined by you or by the number of degree of freedom you have). As inactive main effects variability is then pooled into the error variance, p-values may be susceptible to change in the process and end up being above the threshold you specified, even if originally selected.
Something similar may happen in stage 2, where a subset of 2nd order effects is tested to see if there is an improvement of the model RMSE when adding these effects (even if they may not be all statistically significant).
Two things to consider with caution :
- Statistical significance principle : The 0.05 p-value threshold is not a cut-off value, as effects just above this value may also be interesting to consider in the model (due to domain expertise, or the use of other modeling method not based on p-values). Also statistical significance doesn't give you any information about effect importance/size.
- A model is just a representation of the experimental reality you recorded. If you try different modeling techniques, using Generalized Regression platform with different Estimation methods (Two-stage forward selection, Pruned Forward selection, ...) and a different validation criterion (like information criteria AICc and BIC), you may end up with different models. It's always interesting to compare several approaches to see how the different models may be similar or differ, and use domain expertise to proceed with the most reasonable one(s).
I hope this answer will help you,
"It is not unusual for a well-designed experiment to analyze itself" (Box, Hunter and Hunter)
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Significance of factors in Definitive Screening Design
Hi @Ahmedhadi,
Welcome in the Community !
It is difficult to help you without looking at your design and without knowing how you design it.
Nevertheless, I think you may find answers in this Help section about the analysis of DSDs : Statistical Details for the Fit Definitive Screening Platform (jmp.com)
You might also be interested in the original publication of the Fit DSD method : Bradley Jones & Christopher J. Nachtsheim (2016): Effective Design-Based Model Selection for Definitive Screening Designs, Technometrics, DOI: 10.1080/00401706.2016.1234979
As you can see on the screenshot, the analysis of DSDs is done in 2 steps to take into account the specific structure of DSD :
- First stage involves main effects identification with the responses values
- Second stage involves 2-factors interactions and quadratic effects identification (based on Effects Heredity principle) with the responses residuals from the first stage model.
From the low amount of information provided, if your 37 runs DSDs involves 15 continuous factors, you may have 4 extra runs in your design, so in your stage 1, the variance from the supposed model (with all main effects) is estimated against error variance from the 4 extra runs. This enable to identify active effects below a certain p-value threshold (defined by you or by the number of degree of freedom you have). As inactive main effects variability is then pooled into the error variance, p-values may be susceptible to change in the process and end up being above the threshold you specified, even if originally selected.
Something similar may happen in stage 2, where a subset of 2nd order effects is tested to see if there is an improvement of the model RMSE when adding these effects (even if they may not be all statistically significant).
Two things to consider with caution :
- Statistical significance principle : The 0.05 p-value threshold is not a cut-off value, as effects just above this value may also be interesting to consider in the model (due to domain expertise, or the use of other modeling method not based on p-values). Also statistical significance doesn't give you any information about effect importance/size.
- A model is just a representation of the experimental reality you recorded. If you try different modeling techniques, using Generalized Regression platform with different Estimation methods (Two-stage forward selection, Pruned Forward selection, ...) and a different validation criterion (like information criteria AICc and BIC), you may end up with different models. It's always interesting to compare several approaches to see how the different models may be similar or differ, and use domain expertise to proceed with the most reasonable one(s).
I hope this answer will help you,
"It is not unusual for a well-designed experiment to analyze itself" (Box, Hunter and Hunter)
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Significance of factors in Definitive Screening Design
Dear Victor,
Thank you so much for your detailed and helpful response and sorry for not providing all the information.
Of course, I have 15 "continuous" factors and I have included 4 extra runs as recommended. For now, I am only interested in determining the dominating factors that significantly influence the response. Therefore, I will consider all the "active factors" listed by the software in Stage 1 as significant.
Regarding comparing different models, I found it tricky to do so for some models since there is no R-squared value to evaluate/compare the models. Is there a systematic way of doing that?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Significance of factors in Definitive Screening Design
Hi @Ahmedhadi,
If you want to compare and select the most "sensible" models, I would recommend compare them with another metric than R² (or R² adjusted), since R² takes only in consideration the proportion of variance explained by the model but not its complexity, so if you add more and more terms, you may end up with an higher R² but you'll have a more complex model that may fit some noise in it.
An information criterion, like AICc or BIC, and/or Maximum Likelihood if you need a different response distribution than the normal one, can be more effective for comparing and selecting models, as they balance the accuracy of the model with its complexity (number of terms included in the model).
You don't need necessarily to try all the possible combination of terms for comparing and selecting the models, as Generalized Regression (JMP Pro) with the different estimation methods and validation criterion is a semi-automated process (each method will stop when reaching the "best" model). More infos here : Generalized Regression Models (jmp.com)
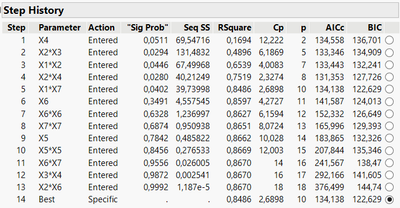
You may also look in the Stepwise platform (in the Fit Model platform, changing the personality to Stepwise), where you can screen "automatically" the possible terms in your model and select the most informative one thanks to a stoping rule/criterion (based on BIC, AICc, p-value threshold, etc... I recommend using information criterion like AICc or BIC). The nice part is that you can follow the different steps involved during the different models creation, and how each step had an impact on the model's quality (in terms of R² and AICc / BIC) :
It works quite well, but you may need after all some model fine-tuning, as it can be a greedy approach (it will enter every term that may provide a positive impact for the model).
More infos here : Stepwise Regression Models (jmp.com)
There is also an option to try "All Possible Models", but given the high number of factors you have (and even higher number of possible terms when taking into consideration 2nd order terms), I wouldn't recommend it as it will be too long and too computationally expensive.
I hope this answer will help you,
"It is not unusual for a well-designed experiment to analyze itself" (Box, Hunter and Hunter)
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Significance of factors in Definitive Screening Design
Another point to consider is that the software or algorithm does not claim to find the best model. They help to eliminate many bad models from further selection. Different methods for selecting a model can yield different solutions. The information provided with a solution should help guide you to improvements. Choosing which terms to include is up to you, not software.
You might try another selection method to see if the solution is better suited to your needs. JMP provides many such methods.
Recommended Articles
- © 2026 JMP Statistical Discovery LLC. All Rights Reserved.
- Terms of Use
- Privacy Statement
- Contact Us