- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Discussions
Solve problems, and share tips and tricks with other JMP users.- JMP User Community
- :
- Discussions
- :
- Re: Setting Stage 1 P value in Analyis of DSD at a high level to dedect active e...
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Setting Stage 1 P value in Analyis of DSD at a high level to detect active effects
I have a question on the setting of Stage 1 P value for analysis of a 7-factor DSD in attachment.
I need to set the stage 1 P value at 0,4 to detect the 5 active factors, while the default setting is 0,05; is there an explanation?
Is the stage 1 P default of 0,05 not too low? How to set stage 1 P, is there a rule of thumb?
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Setting Stage 1 P value in Analyis of DSD at a high level to dedect active effects
Hi @frankderuyck,
I guess the example you show is for education/training purpose since the response is based on a formula ?
A good reminder from JMP Help to answer your question is : "A minimum run-size DSD is capable of correctly identifying active terms with high probability if the number of active effects is less than about half the number of runs and if the effects sizes exceed twice the standard deviation" (Source: Overview of the Fit Definitive Screening Platform)
In your case, you have 7 factors and expect 5 to be detected as "active", so it's a very complex task to perform when using a minimum run-size DSD with a relative high response noise.
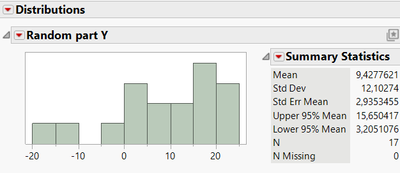
When I look at the "noise"/variability part of your response formula, I can see that the random uniform part is quite large (from -25 to 25) compared to the size of the estimates (from -20,8 to 5,2) for the factors you want to detect in this first stage. So for most factors for which you have specified an effect size to estimate, it might be very hard to detect them and estimate their effect size, compared to the noise/variability part that you have added in the formula. You also mention 5 "active" factors, but I think there is a confusion : they will be only considered "active" only if their relative size of estimates are large enough compared to noise/natural variability of your experiments. It is not because you have specified an estimate different from 0 that they should be considered as active/important. It's a question of signal-to-noise ratio, and a difference between statistical significance and practical significance.
The significance level (p-value threshold) to adjust could be estimated depending on your design and assumed noise (anticipated RMSE) in the Evaluate Designs platform. In this platform, you can adjust significance level and Anticipated RMSE to evaluate the power (probability to detect an effect if active).
Perhaps not "exactly rigorous", but as an exercice, you can check if the outputs from your analysis seem right as you're working on a theoritical response formula. When adding a new formula column to look at the noise part of the formula, I can estimate a standard deviation of approximately 12 :
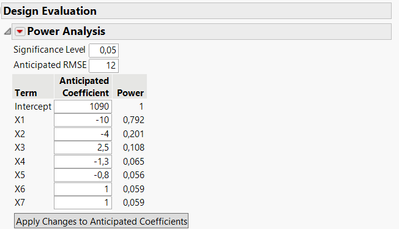
When using this value as Anticipated RMSE (probably as a low estimate for RMSE), fixing the significance level at 0.05 and using the theoritical estimates of the formula as Anticipated coefficients (I left "1" for the null effects of your formula to see the power "baseline" of your design for main effects with this RMSE), it matches the outputs from your analysis :
Only X1 has an effect size large enough to be detected with a high probability. The other effects have a relatively too low effect size (compared to the Anticipated RMSE of the response). If you have a higher significance threshold with the same expected noise, the power to detect main effects will increase :
Several options (alone or combined) for your example could be used depending on your teaching objectives :
- You can reduce the variability (random uniform part in the Y formula response), to make sure you can detect most of the active effects you want to detect (and estimate).
- You can increase design size, to enable easier detection of active effects. From JMP Help : "However, by augmenting a minimum run-size DSD with four or more properly selected runs, you can identify substantially more effects with high probability." : Overview of the Fit Definitive Screening Platform
- You can increase effect size (size of the factors estimates in the formula), so that it becomes easier to detect effect despite the high noise/variability.
- You can also try different analysis platforms to detect the main effects. The Fit Two Level Screening Platform may offer a different perspective for example :
- No matter what you choose, the Evaluate Designs platform (and Compare Designs platform to compare different designs choice) is really important to show and explain to students, as it enables to better assess the pros and cons of any design depending on the objectives, complexity of the model, ability to detect effect, aliasing properties, etc... It can also be used to assess the significance level to adjust if you have prior information about anticipated RMSE and anticipated coefficients.
I hope my answer will help you understand what's going on in your example,
"It is not unusual for a well-designed experiment to analyze itself" (Box, Hunter and Hunter)
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Setting Stage 1 P value in Analyis of DSD at a high level to dedect active effects
Hi @frankderuyck,
I guess the example you show is for education/training purpose since the response is based on a formula ?
A good reminder from JMP Help to answer your question is : "A minimum run-size DSD is capable of correctly identifying active terms with high probability if the number of active effects is less than about half the number of runs and if the effects sizes exceed twice the standard deviation" (Source: Overview of the Fit Definitive Screening Platform)
In your case, you have 7 factors and expect 5 to be detected as "active", so it's a very complex task to perform when using a minimum run-size DSD with a relative high response noise.
When I look at the "noise"/variability part of your response formula, I can see that the random uniform part is quite large (from -25 to 25) compared to the size of the estimates (from -20,8 to 5,2) for the factors you want to detect in this first stage. So for most factors for which you have specified an effect size to estimate, it might be very hard to detect them and estimate their effect size, compared to the noise/variability part that you have added in the formula. You also mention 5 "active" factors, but I think there is a confusion : they will be only considered "active" only if their relative size of estimates are large enough compared to noise/natural variability of your experiments. It is not because you have specified an estimate different from 0 that they should be considered as active/important. It's a question of signal-to-noise ratio, and a difference between statistical significance and practical significance.
The significance level (p-value threshold) to adjust could be estimated depending on your design and assumed noise (anticipated RMSE) in the Evaluate Designs platform. In this platform, you can adjust significance level and Anticipated RMSE to evaluate the power (probability to detect an effect if active).
Perhaps not "exactly rigorous", but as an exercice, you can check if the outputs from your analysis seem right as you're working on a theoritical response formula. When adding a new formula column to look at the noise part of the formula, I can estimate a standard deviation of approximately 12 :
When using this value as Anticipated RMSE (probably as a low estimate for RMSE), fixing the significance level at 0.05 and using the theoritical estimates of the formula as Anticipated coefficients (I left "1" for the null effects of your formula to see the power "baseline" of your design for main effects with this RMSE), it matches the outputs from your analysis :
Only X1 has an effect size large enough to be detected with a high probability. The other effects have a relatively too low effect size (compared to the Anticipated RMSE of the response). If you have a higher significance threshold with the same expected noise, the power to detect main effects will increase :
Several options (alone or combined) for your example could be used depending on your teaching objectives :
- You can reduce the variability (random uniform part in the Y formula response), to make sure you can detect most of the active effects you want to detect (and estimate).
- You can increase design size, to enable easier detection of active effects. From JMP Help : "However, by augmenting a minimum run-size DSD with four or more properly selected runs, you can identify substantially more effects with high probability." : Overview of the Fit Definitive Screening Platform
- You can increase effect size (size of the factors estimates in the formula), so that it becomes easier to detect effect despite the high noise/variability.
- You can also try different analysis platforms to detect the main effects. The Fit Two Level Screening Platform may offer a different perspective for example :
- No matter what you choose, the Evaluate Designs platform (and Compare Designs platform to compare different designs choice) is really important to show and explain to students, as it enables to better assess the pros and cons of any design depending on the objectives, complexity of the model, ability to detect effect, aliasing properties, etc... It can also be used to assess the significance level to adjust if you have prior information about anticipated RMSE and anticipated coefficients.
I hope my answer will help you understand what's going on in your example,
"It is not unusual for a well-designed experiment to analyze itself" (Box, Hunter and Hunter)
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Setting Stage 1 P value in Analyis of DSD at a high level to dedect active effects
Hi Victor, thanks again for your detailed reply. Yes it is a DOE training case based on a pilot case study where results were blurred with considerable noise and experiment budget was limited to maximum 25 runs. Unfortunately there was no preleminary knowledge and a pragmatic approach wis required. Main goal of this screening study is to specify the strong main effects with which the DSD can be augmented to get an RSM. That's why I did not include the 4 extra DSD runs and kept 17 as such there are 8 spare runs to augment (4 spare runs might be too low).
Interesting to notice is that by increasing the treshold P to 0,4 the DSD analysis still detects 5 significant factors! Only when the threshold P is as high as 0,7 the 2 smaller, non significant effects X6 and X7 come in and (like in ROC analysis) the model specificity decreases. Augmenting the 17 run DSD to 24 using the 5 strong effect results in a very good and useful model and succesful achievement of experimental goal (match Y target).
I like very much the Fit two level Screening Platform you mention above, I would also select the X4.
This case study shows that using a pragmatic approach, even with noisy results and budget constraint a DSD still is a powerful screening tool as the "S" stands for. I still use it a lot.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Setting Stage 1 P value in Analyis of DSD at a high level to dedect active effects
Also SVEM forward selection does a good job! cfr. attachment
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Setting Stage 1 P value in Analyis of DSD at a high level to dedect active effects
Hi @frankderuyck,
I have mixed feelings on the output and (systematic) use of SVEM, particularly on noisy data.
SVEM forward selection does not "select" terms in the model (or filter them thanks to a specific statistical criterion and threshold), but instead try to estimate them as precisely as possible thanks to the data points resampling with various training/validation anticorrelated weights. By default, every terms will be considered and estimated with SVEM.
So if your objective is about understanding and filtering the main important effects through screening, SVEM might not help you further, as you're lacking a decision framework (statistical criterion, metric and threshold) to do this. SVEM is however very helpful in a predictive mindset, for precise terms estimation.
However :
- You could use the column/metric "Percent NonZero" as a statistical metric to refine the model, but you'll have the same difficulty as with p-values to define a threshold : should a term be >50% non-zero to be included in the model and considered "active" ? Or another level ?
- By visualizing the data from SVEM model, you can probably highlight some key effects and select them based on practical importance (for example, absolute value of the term should be > 2) :
But again, the definition of this "acceptance" threshold may involve a lot of domain expertise and thinking to not exclude prematurely some terms that could be interesting to investigate further.
Also if you look at the residuals pattern, something strange happen :
I would not trust a regression model that shows this non-random residuals pattern (bias). But this can be "improved" by lowering the model complexity, if you launch SVEM GenReg only with main effects :
It seems there might be a curvature in the residual pattern. So obviously in your example, interactions and quadratic effects of your response formula are not investigated here in this simple model, and that can explain this curvature pattern.
I don't think complexifying model building and estimation is the thing to do, particularly with noisy data like in this example.
Your model quality will always be linked to the quality (and precision) of your data.
"It is not unusual for a well-designed experiment to analyze itself" (Box, Hunter and Hunter)
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Setting Stage 1 P value in Analyis of DSD at a high level to dedect active effects
I agree, a regression model based on initial screening can't be trusted at all; this is not the objective of screening that just gives a direction how to further proceed in a sequential workflow. All thee analysis tools above, DSD analysis, two level fit and SVEM filter out the same 5 strongest effects that can be used in augmenting the DSD. I like the sequential approach; to build a house of knowledge one should start with the stongest building blocks to get a solid framework for studying the other smaller important effects.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Setting Stage 1 P value in Analyis of DSD at a high level to dedect active effects
In this 2-level screening there is a strong, significant quadratic effect; is this reliable? As this screening platform only checks 2 levels how can it detect 3-level quadratic effects?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Setting Stage 1 P value in Analyis of DSD at a high level to dedect active effects
Hi @frankderuyck,
You can find guidelines and more info in the documentation: Overview of the Fit Two Level Screening Platform
You can also check the order of terms/effects introduction in the model here : Statistical Details for Order of Effect Entry
This platform is not recommended for multi-levels categorical or ordinal factors, as they will be treated as continuous.
For quadratic effects, most of the time these effects will be artificially orthogonalized to enter the model, so p-values and effects estimation may be imprecise. But the platform can still detect high contrast quadratic effects for 3-levels continuous factors.
I used this platform in this topic : Découverte des plans OML (Orthogonal Main Effects Screening Designs for Mixed Le... - JMP User Commu... and it helped me detect a quadratic effect that was not detected by Fit Definitive Screening platform or by two estimation methods from Fit Model (Generalized Regression) platform.
So it can be interesting to test the Fit Two-Levels platform (and following the guidelines and recommendations) to compare models from different platforms and understand which ones agree/disagree about terms selection, and what are the most relevant models.
Hope this answer may help you,
"It is not unusual for a well-designed experiment to analyze itself" (Box, Hunter and Hunter)
Recommended Articles
- © 2026 JMP Statistical Discovery LLC. All Rights Reserved.
- Terms of Use
- Privacy Statement
- Contact Us