- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Discussions
Solve problems, and share tips and tricks with other JMP users.- JMP User Community
- :
- Discussions
- :
- Re: Segmented standard least squares regression
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Segmented standard least squares regression
How can I perform a standard least square regression at specific values of my x axis?
For more context - I plot voltage against current and at values -10A -5A 5A 10A I need a standard least regression model of so many points around these values. I imagine getting either 4 dots or 4 small lines on my data to represent this.
I have JMP 17 pro and currently do it for all of the data set however this is not what I need.
A method to do this through JMP analysis is preferred over script but anything would be great :)
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Segmented standard least squares regression
Hi @MedianRooster10 ,
Thanks for the data table, that helps to understand things a bit better.
If you don't need to do a least squares fit for all of your data, but just a certain segment or multiple segments, I still think that using some kind of identifying column is the way to go and use that in the model as either a BY variable or as a local data filter. I'm also guessing that you might have to do this for many data tables or columns, which means scripting actually would be a pretty good way to go about it.
If you wanted to do it with a little scripting and the rest interfacing with JMP, below is a little code that will sort your data table, make a new data table, generate a column called :Segment and then assign a value to the segment of choice. In the code, the target is the target current value -- I chose 10, and range is the number of data points on either side of it. if you then do a regular standard least squares and use the :Segment column as a local data filter, you can then select segment 2 and get the least squares fit for the data.
Names Default To Here( 1 );
Current Data Table() << Sort( By( :"Current(A)"n ), Order( Ascending ), Output Table( "Sorted.jmp" ) );
dt = Data Table("Sorted");
dt << New Column( "Segment", "Continuous", "Ordinal" );
range = 5; //rows to group on either side of target
target = 10; //5A
rows = Current Data Table() << Get Rows Where( (:"Current(A)"n >= target - 0.3 & :"Current(A)"n <= target + 0.3) );
For( i = 1, i <= N Rows(dt), i++,
If(
i < rows - range, :Segment[i] = 1,
(i >= rows - range & i <= rows + range), :Segment[i] = 2,
i > rows + range, :Segment[i] = 3
)
);You get an output that looks something like this.
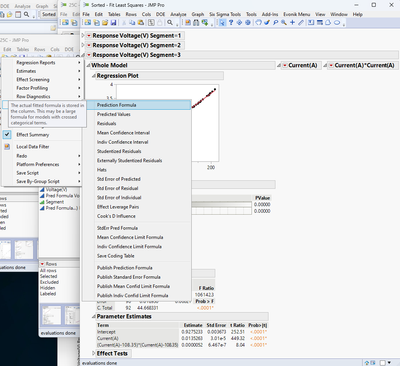
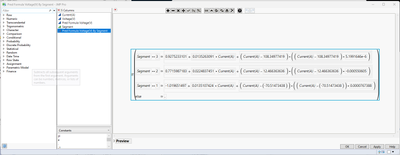
If you use the Segment column as a BY variable in the SLS model fit, when you get your model of the data, you can then hold down the CTRL key and left click the red hot button near one of the "Response Voltage" names and select Save Columns > Prediction Formula, and this will save a prediction formula column to the data table where a different equation is used, depending on the segment number.
Now, that's certainly one way to do it.
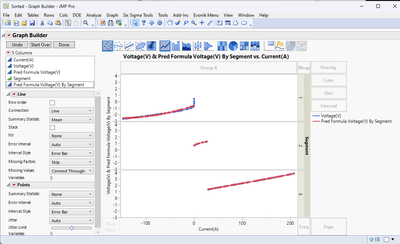
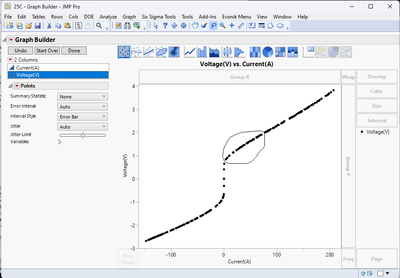
Another way you could do it is by making your graph of the voltage vs current in graph builder, then using the lasso tool (next to the magnifying glass, under the menus) to select the the data you want to fit.
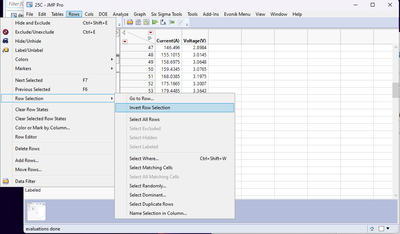
Then go Rows > Row Selection > Invert Row Selection.
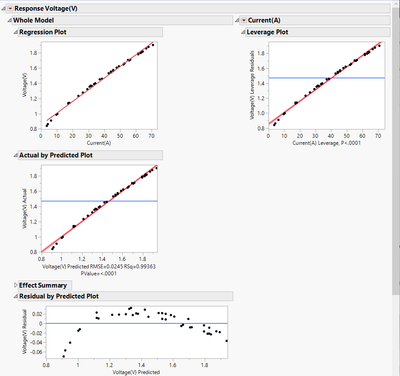
Then right click on one of the row numbers and select Hide and Exclude. Then, when you go to the Model platform for your standard least squares, you can model just those data points that aren't hidden and excluded.
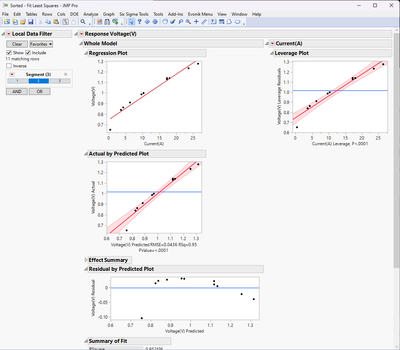
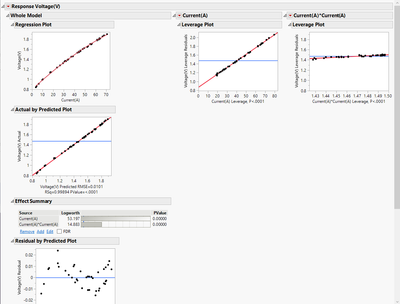
In the below example, you can see the model and the SLS fit to the data. From the Residual by Predicted Plot, you can see some curvature, so I added a Current*Current term, and you get a much better fit with slightly more random residuals.
If you do know the functional form of the formula for the different piecewise sections of your data, then I'd go about it the way Victor mentioned using the Nonlinear platform. But, you need to know the functional form of each piece and know where to "slice" up the data.
Between this and what Victor posted, you should have enough to get started.
Hope this helps!,
DS
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Segmented standard least squares regression
Hi @MedianRooster10 ,
Are you able to share a sample data table so we can see how the data is structured? This might help to come to a solution faster.
One idea that came to mind is that you have a column categorized the different current groups as a nominal data type. You might have for the :Current column numerical values, like -10, -5, 5, 10, but you could have a column with text like -10A -5A 5A 10A, for each grouping of current and then when you do your standard LS regression, you use this column as the "BY" variable.
It would be like using the Big Class.jmp file and modeling :height as Y, :weight as X, and then :sex as the "BY" variable. This would provide you a model for all the Y's grouped into those different voltage ranges. This might not be what you're after, but again, it would help to get an example data table to see how your data is structured and provide a more specific solution.
Hope this helps!,
DS
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Segmented standard least squares regression
Hi @SDF1
I don't think that is what I am after.
I have attached a subset of the data for 1 temperature and the graph I produce.
Its not a linear graph however I do want a partial linear regression. For example I want to take the 10 closest data points to 5A and calculate the least min square of this (plot this as a data point on my graph).
Thank you for your help!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Segmented standard least squares regression
Hi @MedianRooster10,
I think you're trying to do a piecewise regression. You may be able to do it with the Functional Data Explorer, or with the Nonlinear platform.
This JMP Blog might help you realize this regression type on a very similar use case : Fitting piecewise functions with JMP's Nonlinear platform
Hope this will help you,
"It is not unusual for a well-designed experiment to analyze itself" (Box, Hunter and Hunter)
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Segmented standard least squares regression
Hi @MedianRooster10 ,
Thanks for the data table, that helps to understand things a bit better.
If you don't need to do a least squares fit for all of your data, but just a certain segment or multiple segments, I still think that using some kind of identifying column is the way to go and use that in the model as either a BY variable or as a local data filter. I'm also guessing that you might have to do this for many data tables or columns, which means scripting actually would be a pretty good way to go about it.
If you wanted to do it with a little scripting and the rest interfacing with JMP, below is a little code that will sort your data table, make a new data table, generate a column called :Segment and then assign a value to the segment of choice. In the code, the target is the target current value -- I chose 10, and range is the number of data points on either side of it. if you then do a regular standard least squares and use the :Segment column as a local data filter, you can then select segment 2 and get the least squares fit for the data.
Names Default To Here( 1 );
Current Data Table() << Sort( By( :"Current(A)"n ), Order( Ascending ), Output Table( "Sorted.jmp" ) );
dt = Data Table("Sorted");
dt << New Column( "Segment", "Continuous", "Ordinal" );
range = 5; //rows to group on either side of target
target = 10; //5A
rows = Current Data Table() << Get Rows Where( (:"Current(A)"n >= target - 0.3 & :"Current(A)"n <= target + 0.3) );
For( i = 1, i <= N Rows(dt), i++,
If(
i < rows - range, :Segment[i] = 1,
(i >= rows - range & i <= rows + range), :Segment[i] = 2,
i > rows + range, :Segment[i] = 3
)
);You get an output that looks something like this.
If you use the Segment column as a BY variable in the SLS model fit, when you get your model of the data, you can then hold down the CTRL key and left click the red hot button near one of the "Response Voltage" names and select Save Columns > Prediction Formula, and this will save a prediction formula column to the data table where a different equation is used, depending on the segment number.
Now, that's certainly one way to do it.
Another way you could do it is by making your graph of the voltage vs current in graph builder, then using the lasso tool (next to the magnifying glass, under the menus) to select the the data you want to fit.
Then go Rows > Row Selection > Invert Row Selection.
Then right click on one of the row numbers and select Hide and Exclude. Then, when you go to the Model platform for your standard least squares, you can model just those data points that aren't hidden and excluded.
In the below example, you can see the model and the SLS fit to the data. From the Residual by Predicted Plot, you can see some curvature, so I added a Current*Current term, and you get a much better fit with slightly more random residuals.
If you do know the functional form of the formula for the different piecewise sections of your data, then I'd go about it the way Victor mentioned using the Nonlinear platform. But, you need to know the functional form of each piece and know where to "slice" up the data.
Between this and what Victor posted, you should have enough to get started.
Hope this helps!,
DS
Recommended Articles
- © 2026 JMP Statistical Discovery LLC. All Rights Reserved.
- Terms of Use
- Privacy Statement
- Contact Us