- JMP will suspend normal business operations for our Winter Holiday beginning on Wednesday, Dec. 24, 2025, at 5:00 p.m. ET (2:00 p.m. ET for JMP Accounts Receivable).
Regular business hours will resume at 9:00 a.m. EST on Friday, Jan. 2, 2026. - We’re retiring the File Exchange at the end of this year. The JMP Marketplace is now your destination for add-ins and extensions.
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Discussions
Solve problems, and share tips and tricks with other JMP users.- JMP User Community
- :
- Discussions
- :
- Sample Size Question
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Sample Size Question
If I know my parts have a 30% failure rate, how many parts do I need to inspect to be 95% confident I will find at least one failure? Assuming I made a process improvement and want to see if my failure rate decreased from 30% to 10% w/ 95% confidence, then how many parts do I need to inspect? I think JMP can give me these answers through the DOE>Sample Size Explorer>Power wizard, but I'm not exactly sure how to use this script to get the answers to these pretty basic sample size questions.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Sample Size Question
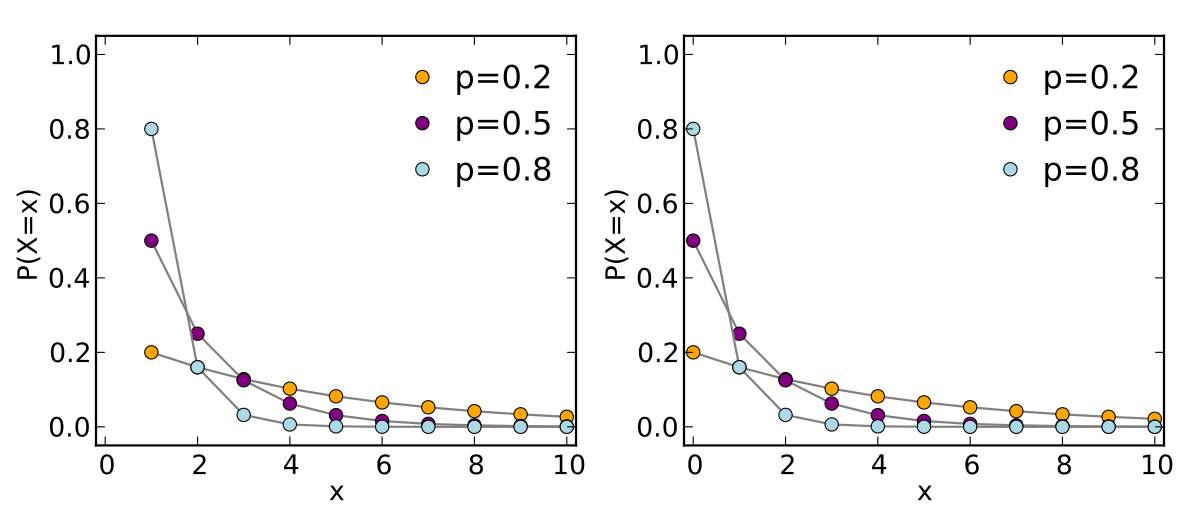
Agreed @dlehman1 ! And, for completeness and for everyone's further understanding: For the geometric distribution, the way "Random Geometric (p)" is parameterized in JMP (returns the number of non-failures until a failure occurs, for failures with probability p), the mean is (1-p)/p. So, for p=0.3 the mean is (1-0.3)/0.3 = 2.3. And for p=0.1, the mean is (1-0.1)/0.1 = 9. And, these verify your simulations where you estimated the means as 2.3487 and 8.951, respectively.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Sample Size Question
Well, the files gives 95% confidence intervals for the mean number of parts before the first defect shows up. If it takes 4 hours to inspect each part, then multiply the mean number of parts (and/or the confidence interval) by 4 hours. I think I may be missing something in your question, but that is what I would say.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Sample Size Question
Thanks dlehman1 and MRB3855 as both of these do end up giving me what I was looking for as I now have a few tools to add to my JMP toolbox. I appreciate the formula supplied by MRB3855 (Samples to test to be 95% confident you find a reject = ln(0.05)/ln(1-p) where p is the reject rate which was 0.3 (30%) or 0.1 (10%), then round n up to the nearest integer) to get the answer to my basic question (9 and 29, respectively).
The geometric distribution was a new thing for me (thanks again for the additional explanation of that distribution MRB3855) and simulating this distribution as done in the sample file supplied by dlehman1 was an elegant statistics approach to my question which helps join the statistics vs probability component of this question. Taking this approach a little further, I highlighted the data points around the 95% confidence level, then subset that data, which has its own distribution with a Mean approximately equal to the number supplied by the formula above. Note, for anybody following along here, this mean number is much different than the Mean of these two randomly generated Geometric distributions as their Means are based on the whole distribution for how many parts you will need to inspect on average to find a single failure versus how many parts you need to inspect to be 95% confident you will find a single reject.
Perhaps a small challenge to this awesome JMP community would be if somebody can take this information and make a cool add-in script whereby people with a more limited understanding of statistics and probability can answer my initial question, so they can look smart to their bosses. For example, if the user supplies the Defect Level to Detect and the Confidence Level for detecting a defect, while the script simply outputs the Number of parts to Inspect would be a nice Sample Size calculator. Adding in dlehman1 Geometric distribution idea would be even cooler!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Sample Size Question
Hey @chrsmth!
As it turns out, there does exist a tool in JMP to do the calculation @MRB3855 described for you. It just involves a bit of creative usage.
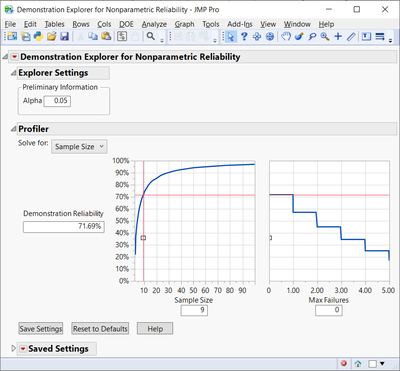
The Nonparametric Demonstration Reliability explorer (DOE>>Sample Size Explorers>>Reliability>>Nonparametric Reliability Demonstration) can easily perform the calculation you need. Just set Max Failures to 0, Alpha to 1-confidence level (in this case, 0.05), make sure the drop-down menu next to Solve for reads Sample Size, and then put 1-p into the Demonstration Reliability box. It should then give you the Sample Size (rounded up the next integer) you need. See the example below:
This explorer is used to determine how many sample sizes you need to demonstrate a given reliability (1-defect rate) while allowing for a maximum number of failures. It is essentially the complement to your situation, where you want to know how many samples you need to demonstrate a given defect rate while allowing for a minimum number of failures. So, in short, it is directly performing the trick @MRB3855 described.
In general, by putting in the complement of the defect rate and one less than the minimum number of defects you would like in the Max Failures entry, you should get the sample size you're looking for in any variation of your situation. Not exactly the direct tool you may have wanted, but if I have described the procedure well enough, this should still answer your question with little effort on your part (you just have to compute 1-p).
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Sample Size Question
Thanks, calking!! I knew JMP had to have this built in somewhere. Now I, along with everybody else who has made it this far in the thread, know how to get the answer to my question using the already built in JMP script.
- « Previous
- Next »
Recommended Articles
- © 2025 JMP Statistical Discovery LLC. All Rights Reserved.
- Terms of Use
- Privacy Statement
- Contact Us