Residuals analysis for multiple linear regressoin-normal quantile plot isn't normal. What to do next?

[#1]

Hello again. This is as much a statistics question as a how-to-use-JMP question.

I've done a Fit Model multiple linear regression on my data and found that only 2 (of possible 6) predictors matter and they interact (So 2 predictors and 1 cross of them in the model).

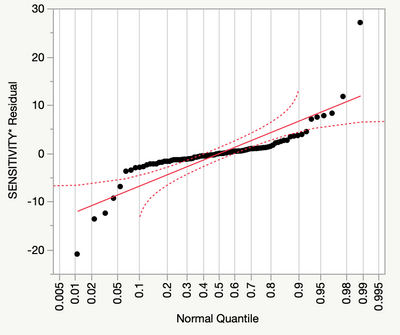
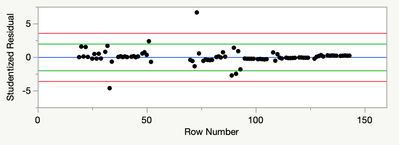
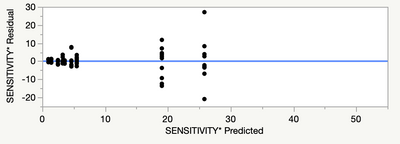
However, my adjusted Rsquare is only 0.72, and my residual analysis looks like this:

Any suggestions for dealing with the non-normality suggested by the quantiles plot? There are no assignable causes for the tail observations on each end to justify excluding them (they are scattered throughout the data), and the highest Cooks-d on an outlier is 0.4.

[#2]

Hi @lisat,

Are your variables normally distributed? Perhaps a transformation prior to linear regression would help.

[#3]

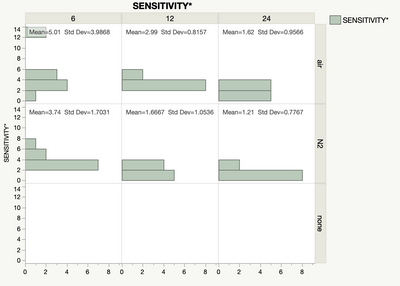
The data are not normally distributed. For each of the categorical factors that are significant, there is a separate non-normal distribution.  (One set of data here is suppressed because it was increasing the bin size, hiding the detail in the other two categories. Basically the same story but with greater spread. Chart labels also suppressed for confidientiality.)

[#4 · Accepted solution]

You might take a look at this wikipedia article, specifically the 'in Regression' section. Transformations are easy in JMP: right click on a column heading and choose 'New Formula Column'.  Make a bunch of different transformations and then analyze each using the distributions platforms to decide which is best.  If you transform your target variable and want to predict it, you just need to 'undo' the transformation by using the inverse transformation on your predicted value.