- JMP will suspend normal business operations for our Winter Holiday beginning on Wednesday, Dec. 24, 2025, at 5:00 p.m. ET (2:00 p.m. ET for JMP Accounts Receivable).
Regular business hours will resume at 9:00 a.m. EST on Friday, Jan. 2, 2026. - We’re retiring the File Exchange at the end of this year. The JMP Marketplace is now your destination for add-ins and extensions.
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Discussions
Solve problems, and share tips and tricks with other JMP users.- JMP User Community
- :
- Discussions
- :
- Re: Questions Regarding Normality Test and Advanced Statistical Analysis
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Questions Regarding Normality Test and Advanced Statistical Analysis
Dear JMP Community,
Greetings, I am a student who has recently begun studying statistics. I have a strong interest in applying the knowledge I've learned in a research project. I apologize in advance if my questions seem basic or inappropriate. Currently, I am conducting research by distributing questionnaires to 406 diabetes patients. The questionnaire consists of gender data (categorical), age data (continuous), and 6 variables with Likert scales, where each variable has its own domain. After inputting the data into MS Excel, I have calculated the total answer scores (continuous), the average value of respondents' answers (continuous), and also performed categorization from variables (categorical). Then, I imported this data into JMP Pro 18.
In the initial stage of analysis, I want to perform a normality test. Regarding this, I have several questions:
1. How do I perform a normality test on the 6 variables and their domains? Do I need to conduct normality tests for all variables and their domains simultaneously or separately? Or do you have any suggestions that I could follow given my current situation where I'm experiencing difficulties with the normality test?
2. What should I do if the data is normally distributed or not normally distributed? This is important because the next stages I plan to conduct are Confirmatory Factor Analysis (CFA) and then Structural Equation Modeling (SEM).I greatly appreciate any input and advice you can provide to help me understand the appropriate steps in analyzing this data.
Thank you for your attention and assistance. Sincerely,
Andy
- Tags:
- windows
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Questions Regarding Normality Test and Advanced Statistical Analysis
Great questions, Andy!
A key assumption underlying maximum likelihood estimation in SEM is that the observed variables come from a multivariate normal distribution. There are a few ways to check this assumption, and usually, visual checks (rather than formal tests of normality) are sufficient. Prior to conducting CFA or SEM, I’d suggest the following checks:
Assess univariate normality with Analyze > Distribution. This platform displays a histogram for each variable. Visually checking histograms is usually sufficient for SEM, but if you’d like, you can also look at QQ plots and conduct formal tests that assess whether each variable comes from a Normal distribution.
- In the Distribution platform, click the red triangle menu for a given variable, then select Continuous Fit > Fit Normal.
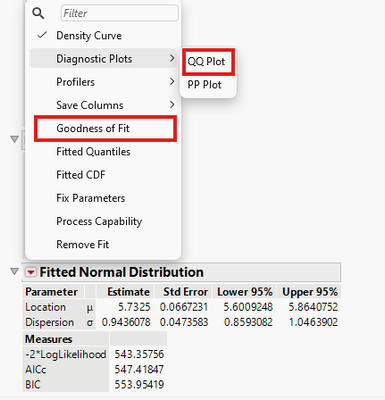
- Then, click the red triangle menu for the Fitted Normal Distribution. To view a QQ plot, select Diagnostic Plots > QQ Plot, and to conduct a formal test of normality (the Shapiro-Wilk test), click Goodness of Fit:
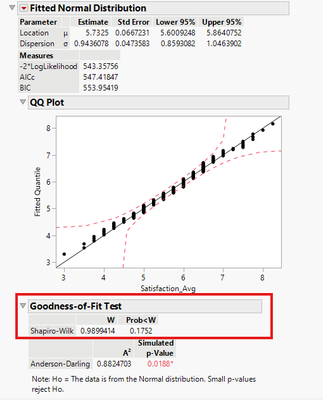
- In the QQ plot, if the observed data closely follow the straight line, that’s good evidence for normality.
- The null hypothesis of the Shapiro-Wilk test is that the observed data come from a Normal distribution. A small p-value means we should reject the null hypothesis; therefore, a nonsignificant p-value is good evidence for normality.
To get a sense of the pairwise relations among your variables, look at bivariate scatterplots with Analyze > Multivariate Methods > Multivariate.
As an additional check, you might also look for multivariate outliers. This can be done from within the SEM platform in JMP Pro. After launching the SEM platform, click on the topmost red triangle menu, and select Launch Explore Outliers:
If these checks indicate that your data are not normally distributed, or are otherwise not well-behaved, you have a few options in the SEM platform. After fitting your model(s), again click on the topmost red triangle menu. Under Inference, there are two options: Robust Inference and Bootstrap Inference. Robust Inference will recompute standard errors (SEs) and model fit statistics using the sandwich correction. This correction results in SEs and fit statistics that are robust to nonnormality. Bootstrap Inference will use bootstrapping to estimate SEs and model fit statistics, and the details of the bootstrapping process (e.g., the number of samples drawn) can be set by the user. These are both viable options to obtain valid inferences in the event that your data are not multivariate normal.
Hope this helps!
Haley
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Questions Regarding Normality Test and Advanced Statistical Analysis
Great questions, Andy!
A key assumption underlying maximum likelihood estimation in SEM is that the observed variables come from a multivariate normal distribution. There are a few ways to check this assumption, and usually, visual checks (rather than formal tests of normality) are sufficient. Prior to conducting CFA or SEM, I’d suggest the following checks:
Assess univariate normality with Analyze > Distribution. This platform displays a histogram for each variable. Visually checking histograms is usually sufficient for SEM, but if you’d like, you can also look at QQ plots and conduct formal tests that assess whether each variable comes from a Normal distribution.
- In the Distribution platform, click the red triangle menu for a given variable, then select Continuous Fit > Fit Normal.
- Then, click the red triangle menu for the Fitted Normal Distribution. To view a QQ plot, select Diagnostic Plots > QQ Plot, and to conduct a formal test of normality (the Shapiro-Wilk test), click Goodness of Fit:
- In the QQ plot, if the observed data closely follow the straight line, that’s good evidence for normality.
- The null hypothesis of the Shapiro-Wilk test is that the observed data come from a Normal distribution. A small p-value means we should reject the null hypothesis; therefore, a nonsignificant p-value is good evidence for normality.
To get a sense of the pairwise relations among your variables, look at bivariate scatterplots with Analyze > Multivariate Methods > Multivariate.
As an additional check, you might also look for multivariate outliers. This can be done from within the SEM platform in JMP Pro. After launching the SEM platform, click on the topmost red triangle menu, and select Launch Explore Outliers:
If these checks indicate that your data are not normally distributed, or are otherwise not well-behaved, you have a few options in the SEM platform. After fitting your model(s), again click on the topmost red triangle menu. Under Inference, there are two options: Robust Inference and Bootstrap Inference. Robust Inference will recompute standard errors (SEs) and model fit statistics using the sandwich correction. This correction results in SEs and fit statistics that are robust to nonnormality. Bootstrap Inference will use bootstrapping to estimate SEs and model fit statistics, and the details of the bootstrapping process (e.g., the number of samples drawn) can be set by the user. These are both viable options to obtain valid inferences in the event that your data are not multivariate normal.
Hope this helps!
Haley
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Questions Regarding Normality Test and Advanced Statistical Analysis
Thank you very much for your help and guidance! I greatly appreciate your quick response and kindness in helping me understand the analysis steps. I will follow your advice and soon send the images of each step's results as soon as possible.
I hope this information can be beneficial to many people. I also hope to communicate with you again after I send the results of each step. Thank you again for your help!
Best regards
Andy
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Questions Regarding Normality Test and Advanced Statistical Analysis
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Questions Regarding Normality Test and Advanced Statistical Analysis
Hi Andy,
Apologies for my delayed reply! Thanks for your patience.
Based on the figures in your included document, I think that proceeding with Robust Inference is a good course of action. Histograms for Age, Diet, and Physical Activity suggest that those variables' departures from normality are not of particular concern, however I noticed that the Medicine variable is very skewed. The skewness in that variable, together with significant Shapiro-Wilk tests, would be good justification for using Robust Inference.
I cannot provide much guidance about whether non-normality in these variables may be a result of a mistake in data collection or analysis. You might double-check that any manual coding or data import was done correctly. Also, keep in mind the content of the questions/items when considering whether skewness makes sense. I will note that non-normally distributed variables are quite common in social science. And as I noted above, the departures from normality in Age, Diet, and PA do not seem to be significant in a practical sense.
When the assumptions underlying Maximum Likelihood estimation in SEM are violated, point estimates are not influenced by those violations; however, standard errors are. Using the Robust Inference option will correct the standard errors such that they are "robust" (i.e., still trustworthy) even if your data violate the assumption of multivariate normality. So, I'd suggest keeping Robust Inference turned on, as you did in your document!
Hope this helps,
Haley
Recommended Articles
- © 2025 JMP Statistical Discovery LLC. All Rights Reserved.
- Terms of Use
- Privacy Statement
- Contact Us