Process capability within sigma estimation for different number of subgroup sizes

[#1]

Dear JMP & Community,

  I'm trying to better understand how JMP estimates the within sigma for different subgroup sizes -- in particular a subgroup of size 1. The online help is somewhat helpful, but I'm hoping to see the equations or have a more clear explanation, as I don't quite see how JMP does it from the description in the online help.

  In the Distribution platform, one has the option of doing process capabilities when you have spec limits for a column. The default setting is to have a subgroup size of 1, and JMP notes that the "Within sigma estimated by average moving range". The online help defines the Average of Moving Range as: "Uses the mean of the moving ranges to estimate sigma. The moving range is the difference between two consecutive points.".

  This doesn't really help me to understand how it performs the estimation/calculation of the within sigma for a subgroup size of 1. Conceptually, it's not easy to see how a single value can have a standard deviation, but this is the default in JMP, vs say a subgroup size of 3 or 5.

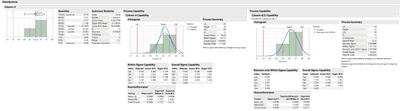
  I've attached a screenshot of the Distribution platform and the default as well as a subgroup size of 3.

  Any feedback would be helpful and much appreciated.

Thanks!,

DS

[#2 · Accepted solution]

See the documentation for the moving range control chart. The moving range determines the range of a span of observations (span is 2 by default). The successive moving ranges are averaged. The mean is divided by a bias correction factor to estimate the sigma. The idea is that the moving range is a short-term estimate and excludes special cause or long-tern variation.

[#3 · Accepted solution]

Hi @Mark_Bailey ,

  Thanks for the reply and hints. That led me to some very helpful and informative internet searches.

  The online JMP help here tells you how it's calculated, so this helps to visualize how it's estimated. Unfortunately, JMP's online documentation doesn't really link all these together, because the discussion on process capability is here, and on moving ranges is here, but it's not easy moving from one subject to the next in a connected fashion.

 Also, it doesn't really explain all too well what d2(n) is for us non-statisticians. But I found a nice post about it here that was easy to follow. I could compute it myself and determine the d2(n) constant for the span n=2. I then tested it out by checking with a subgroup size of 3 and 5, and it worked out. Now it makes sense that under the distribution platform, it gives a warning message when you enter a subgroup size that doesn't divide rationally into the total sample size N, and why for the XBar and R chart why it returns null for the average of the range calculation, even though it graphs the mean in the Range graph below.

  Now it makes a lot more sense. Sometimes it's more helpful to know the step by step math that goes on behind the scenes in JMP in order to explain it to others who also aren't statisticians.

Thanks!,
DS