Probit Analysis & Fit Testing

[#1]

I am using the Simple Probit Analysis script add-in to determine LD50, LD90, and LD95.

Is this script capable of correcting with Abbott's, or how do you set this up?  Currently, I corrected the data myself by applying the Abbott's correction to the raw data to adjust for mortalities.

After running the Probit Add-In, how do I determine goodness of fit?  There are no Chi Squared results.  Is there another way I can run this analysis to get my LD values, as well as getting the Chi Square? 

[#2]

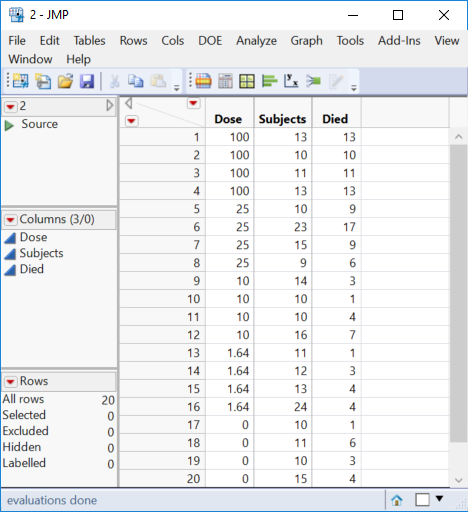
Here is an example of the data:

Dose (% Conc.)	Start (#live)	Mortality @ 15 min. (#dead)
100.00	13	13
100.00	10	10
100.00	11	11
100.00	13	13
25.00	10	9
25.00	23	17
25.00	15	9
25.00	9	6
10.00	14	3
10.00	10	1
10.00	10	4
10.00	16	7
1.64	11	1
1.64	12	3
1.64	13	4
1.64	24	4

I am trying to get LD50/LD90/LD95 results for dosage recommendations. I have this information for 5, 10, and 15 minute applications. 

This is the data for my control:

Dose (% Conc.)	Start (#live)	Mortality (#dead)
0	10	1
0	11	6
0	10	3
0	15	4

[#3]

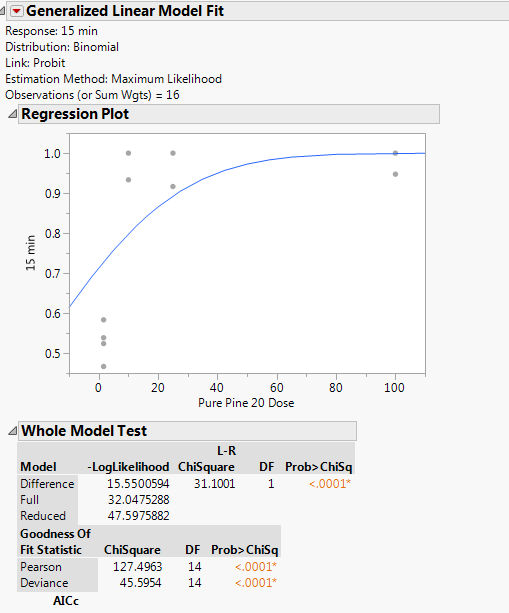
OK, I think I understand now. I was correct to begin with and it is not a survival analysis (life time). We are back to my GLM example but now I will use your data. Here is your data in a JMP data table:

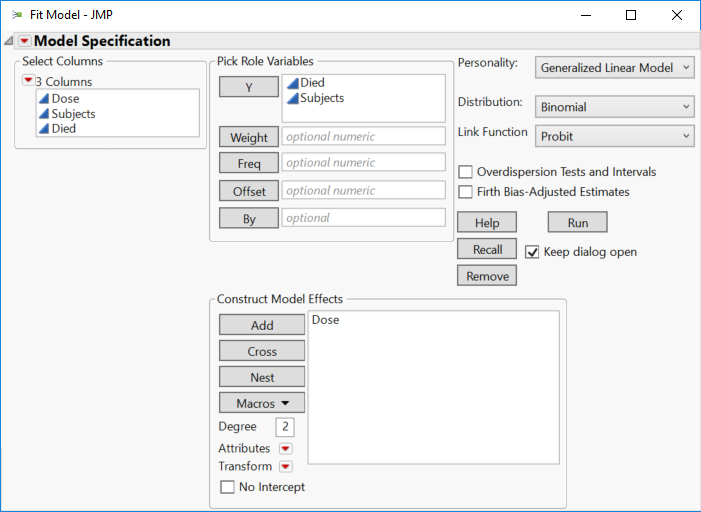
Set up the Fit Model launch dialog as before:

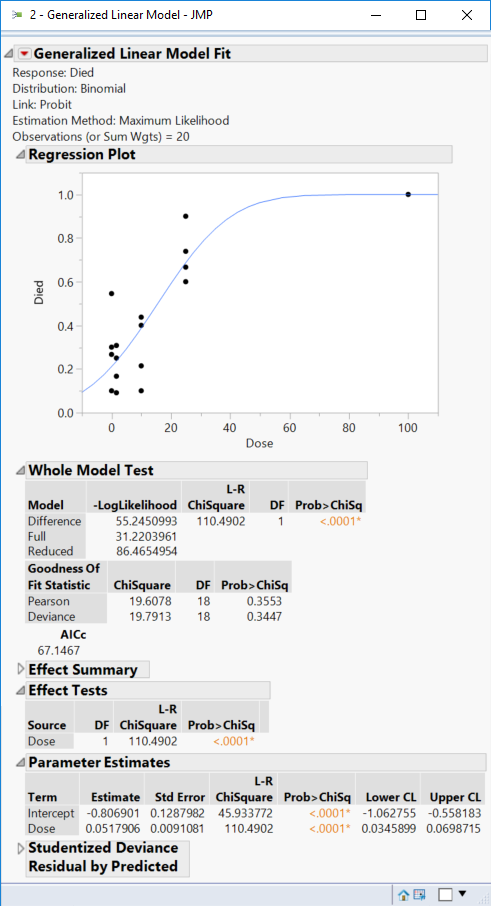
Click Run and then you get these results:

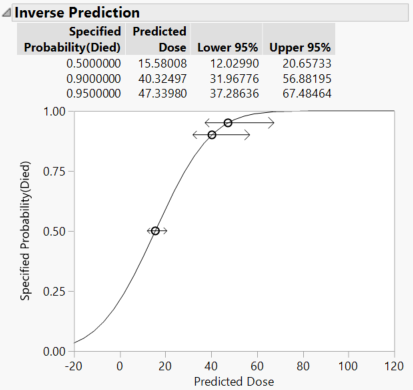
Click the red triangle next to Generalized Linear Model Fit and select Inverse Prediction. Type 0.5 (and any others that you want) for Probability (Died) and click OK.

So now we agree, no?

[#4]

What do I do when some of the models have a bad fit? 

[#5]

• Is it a data problem?
  • Do you have outliers or data errors?
  • Did you accidentally exclude rows that should be included?
• Is it a model problem?
  • Are you using the correct response columns?
  • Are you using the correct predictor column?
  • Is it lack of fit?
• Is it a model assumption problem?
  • Are the errors distributed as expected?
  • Are the errors constant over the entire range of the predictor?

[#6]

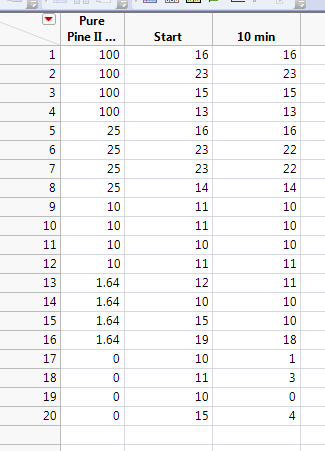
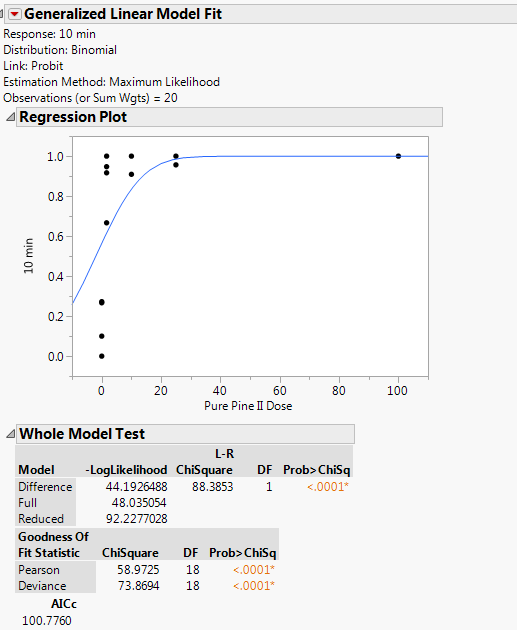
Here is one of the data sets in particular I'm having issues with. If I Hide/Exclude the 0s, the model will fit.

[#7]

You didn't answer any of my questions.

This example must be a different agent than the example that you tested at 15 minutes. It doesn't make sense that the same agent would be that much more lethal with just five more minutes of exposure.

You must use a different dilution/dose range (higher dilution, lower dose) to observe the transition. The highest dose should be 1.64. You should include the zero in the test and in the data analysis. This new data is the only way to fit the probit model for this agent at this time point.

[#8]

(Sorry, I'm being pulled 1000 directions today. :) )

It is a different agent. I tested a total of 6 different agents. I'm being asked to give recommendations at 10 minutes if possible, and 15 minutes as a max. I have a couple of data sets similar to this, where there is very high mortality at doses above 1.64 or 10%.

Why does the model not work in these situations with high mortality at the higher doses?

I think most of it has to do with the data, as I had some strange effects on a couple of the agents. I've had the situation where a lower dose worked more effectively than a higher dose. The model doesn't work in that situation either. A couple at 100 were less effective than lower doses due to evaporation, but the models work fine if I exclude those doses.

In another set, my controls all experience 0 moralities (different species than previous control). Those seem to be causing discrepancies as well.

[#9]

I cannot speak to the discrepancies that you cite, but they call the data into question.

The problem with fitting is that the data exhibits the 'separation' problem. At one level (dose = 0), you have the low response and at all of the other levels (dose > 0), you have the high response. The transition from low to high response is impossible to determine. Try to find LD50 on your own with this data and you will understand the issue. (Does it occur at 0.1? At 0.5? At 1.5?)

You must perform another dose-response test where the dose ranges from 0 to 1.64 in order to fit the probit model and estimate LD50.

[#10]

So is it acceptable at this point to exclude the high responses to get a "fitted" model, which I can use to estimate a predicted dose or range of doses to test as a follow-up? We were not expecting the high response at the very low doses, which is why I have no data for in between. Right now, I need to be able to determine somewhat of a recommendation for these agents, which can be followed up with a secondary study to confirm.

[#11 · Accepted solution]

Excluding the high responses is not acceptable from a modeling or statistics point of view. You are suggesting that you exclude valid data to overcome a basic flaw with the study. (I understand that you could not foresee the potency of this agent, but that does not remove the flaw in the data.) You need more data, between dose = 0 and dose = 1.64, not less data, to solve this problem.

Excluding the high dose samples might be acceptable in your situation but I could not justify it. The fact that you (possibly) obtain a 'better' model this way is not validation. You simply cannot determine the LD50 from this sample of dose-response data except to say that LD50 occurs between 0 and 1.64.