Preparing a Factor Analysis,principal components extraction with varimax rotation

[#1]

Hi everyone, I've been looking at the expertly crafted discussions to learn some basic JMP for my course.

Absolutely full of great information!

However, I'm really stumped at this seemingly easy questions.. Hoping you guys could point me at the right direction.

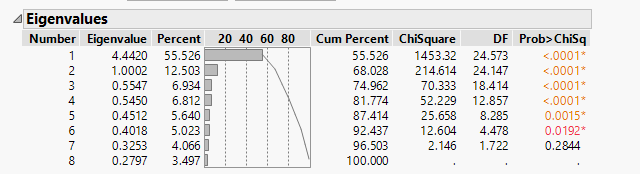
How do I evaluate the appropriateness of using factor analysis by Bartlett’s Test of Sphericity?

For the Factor Analysis to be appropriate, the first test has to be significant correct?

I.E The first test has a ChiSquare of 1453.32, does that make it significant?

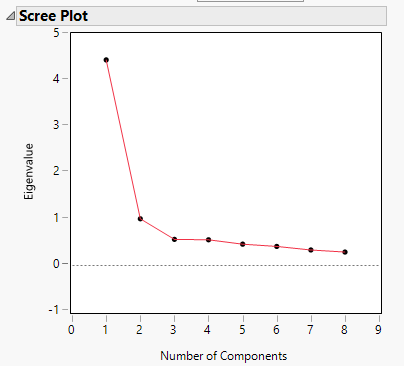
Following that, to compare the number of factors to be extracted based on Eigenvalues, Cumulative Percentage and Scree Plot, I know I need to retain and interpet any component with an eigenvalue greater than 1.00. 

But I'm not sure what I'm supposed to look for in the Cumulative Percentage & Scree plot component.

Please guide the newbie if you can, thank you so much!

[#2 · Accepted solution]

Take a look at the Cumulative Percent Column. 

The idea is that you want to use the smallest number of components to explain the largest amount of variation.

In this case the first two components/factors explain about 68% of the variation. If you want more, you have to add more, but each sucessive step doesn't explain much more.