- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Discussions
Solve problems, and share tips and tricks with other JMP users.- JMP User Community
- :
- Discussions
- :
- Re: Percentile & Goodness-of-fit of Zero Inflated Negative Binomial (ZINB) and N...
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Percentile & Goodness-of-fit of Zero Inflated Negative Binomial (ZINB) and Negative Binomial (NB)
Hi All,
(1) I'd like to get the goodness-of-fit of of Zero Inflated Negative Binomial (ZINB) and Negative binomial (NB) distribution from the following dataset.
(2) I also want to calculate the 95th percentile from the each distribution (ZINB & NB) with JMP 14 or JMP 14 Pro
(3) Is it possible to plot the density functions of ZINB & NB against empirical density of simulated data ? (Y:Cumulative Probability, X:counts)
Thanks in advance. : )
| Sample No. | Data |
| 1 | 0 |
| 2 | 0 |
| 3 | 0 |
| 4 | 0 |
| 5 | 0 |
| 6 | 0 |
| 7 | 0 |
| 8 | 0 |
| 9 | 0 |
| 10 | 0 |
| 11 | 0 |
| 12 | 0 |
| 13 | 0 |
| 14 | 0 |
| 15 | 2 |
| 16 | 0 |
| 17 | 0 |
| 18 | 0 |
| 19 | 0 |
| 20 | 0 |
| 21 | 0 |
| 22 | 0 |
| 23 | 0 |
| 24 | 0 |
| 25 | 0 |
| 26 | 1 |
| 27 | 0 |
| 28 | 0 |
| 29 | 0 |
| 30 | 0 |
| 31 | 0 |
| 32 | 0 |
| 33 | 0 |
| 34 | 0 |
| 35 | 0 |
| 36 | 0 |
| 37 | 0 |
| 38 | 0 |
| 39 | 0 |
| 40 | 0 |
| 41 | 0 |
| 42 | 0 |
| 43 | 0 |
| 44 | 0 |
| 45 | 0 |
| 46 | 0 |
| 47 | 0 |
| 48 | 0 |
| 49 | 0 |
| 50 | 0 |
| 51 | 0 |
| 52 | 0 |
| 53 | 0 |
| 54 | 4 |
| 55 | 0 |
| 56 | 0 |
| 57 | 0 |
| 58 | 0 |
| 59 | 0 |
| 60 | 0 |
| 61 | 0 |
| 62 | 0 |
| 63 | 0 |
| 64 | 0 |
| 65 | 0 |
| 66 | 0 |
| 67 | 0 |
| 68 | 0 |
| 69 | 0 |
| 70 | 2 |
| 71 | 0 |
| 72 | 0 |
| 73 | 0 |
| 74 | 0 |
| 75 | 0 |
| 76 | 0 |
| 77 | 0 |
| 78 | 0 |
| 79 | 0 |
| 80 | 0 |
| 81 | 0 |
| 82 | 0 |
| 83 | 0 |
| 84 | 0 |
| 85 | 0 |
| 86 | 0 |
| 87 | 0 |
| 88 | 0 |
| 89 | 0 |
| 90 | 0 |
| 91 | 0 |
| 92 | 0 |
| 93 | 0 |
| 94 | 0 |
| 95 | 0 |
| 96 | 0 |
| 97 | 0 |
| 98 | 0 |
| 99 | 0 |
| 100 | 0 |
| 101 | 0 |
| 102 | 0 |
| 103 | 0 |
| 104 | 0 |
| 105 | 0 |
| 106 | 0 |
| 107 | 0 |
| 108 | 0 |
| 109 | 0 |
| 110 | 0 |
| 111 | 0 |
| 112 | 0 |
| 113 | 0 |
| 114 | 0 |
| 115 | 0 |
| 116 | 0 |
| 117 | 0 |
| 118 | 0 |
| 119 | 0 |
| 120 | 0 |
| 121 | 1 |
| 122 | 0 |
| 123 | 1 |
| 124 | 0 |
| 125 | 0 |
| 126 | 0 |
| 127 | 0 |
| 128 | 0 |
| 129 | 0 |
| 130 | 0 |
| 131 | 0 |
| 132 | 0 |
| 133 | 0 |
| 134 | 0 |
| 135 | 0 |
| 136 | 0 |
| 137 | 0 |
| 138 | 0 |
| 139 | 0 |
| 140 | 0 |
| 141 | 1 |
| 142 | 0 |
| 143 | 0 |
| 144 | 0 |
| 145 | 0 |
| 146 | 0 |
| 147 | 0 |
| 148 | 0 |
| 149 | 0 |
| 150 | 0 |
| 151 | 0 |
| 152 | 0 |
| 153 | 0 |
| 154 | 0 |
| 155 | 0 |
| 156 | 0 |
| 157 | 0 |
| 158 | 0 |
| 159 | 2 |
| 160 | 0 |
| 161 | 0 |
| 162 | 0 |
| 163 | 0 |
| 164 | 0 |
| 165 | 0 |
| 166 | 0 |
| 167 | 0 |
| 168 | 0 |
| 169 | 0 |
| 170 | 0 |
| 171 | 0 |
| 172 | 0 |
| 173 | 0 |
| 174 | 0 |
| 175 | 0 |
| 176 | 0 |
| 177 | 0 |
| 178 | 0 |
| 179 | 0 |
| 180 | 0 |
| 181 | 0 |
| 182 | 0 |
| 183 | 0 |
| 184 | 0 |
| 185 | 0 |
| 186 | 0 |
| 187 | 0 |
| 188 | 0 |
| 189 | 0 |
| 190 | 0 |
| 191 | 0 |
| 192 | 0 |
| 193 | 0 |
| 194 | 0 |
| 195 | 0 |
| 196 | 0 |
| 197 | 1 |
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Percentile & Goodness-of-fit of Zero Inflated Negative Binomial (ZINB) and Negative Binomial (NB)
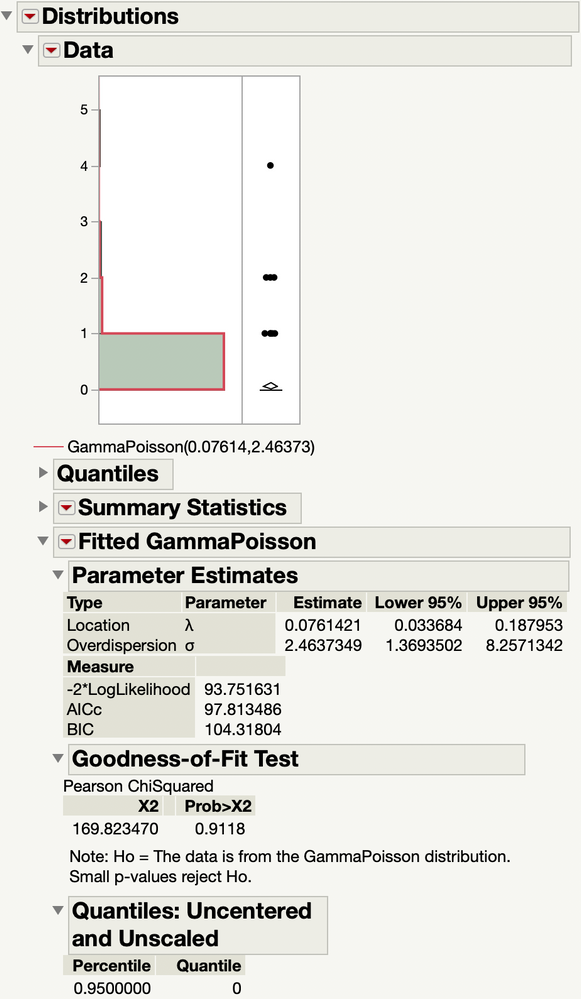
I would normally use the Distribution platform to fit such models but the negative binomial distribution is not one of the choices. Here I modelled your data with the gamma Poisson distribution, obtained the goodness-of-fit test statistics, and estimated the 95% quantile:
It seems to do well.
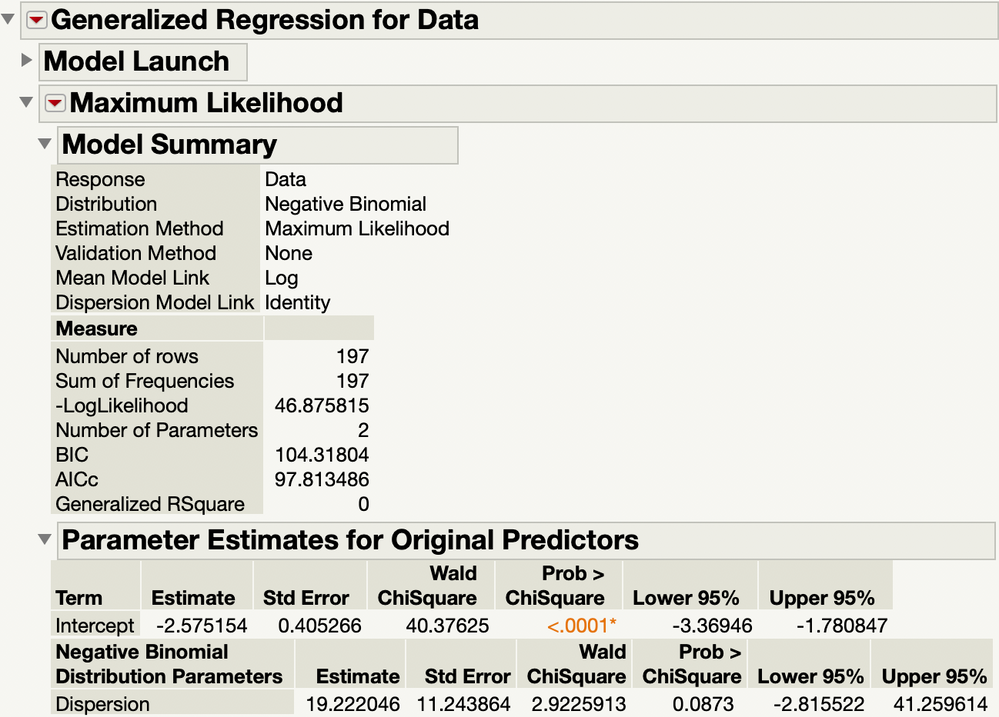
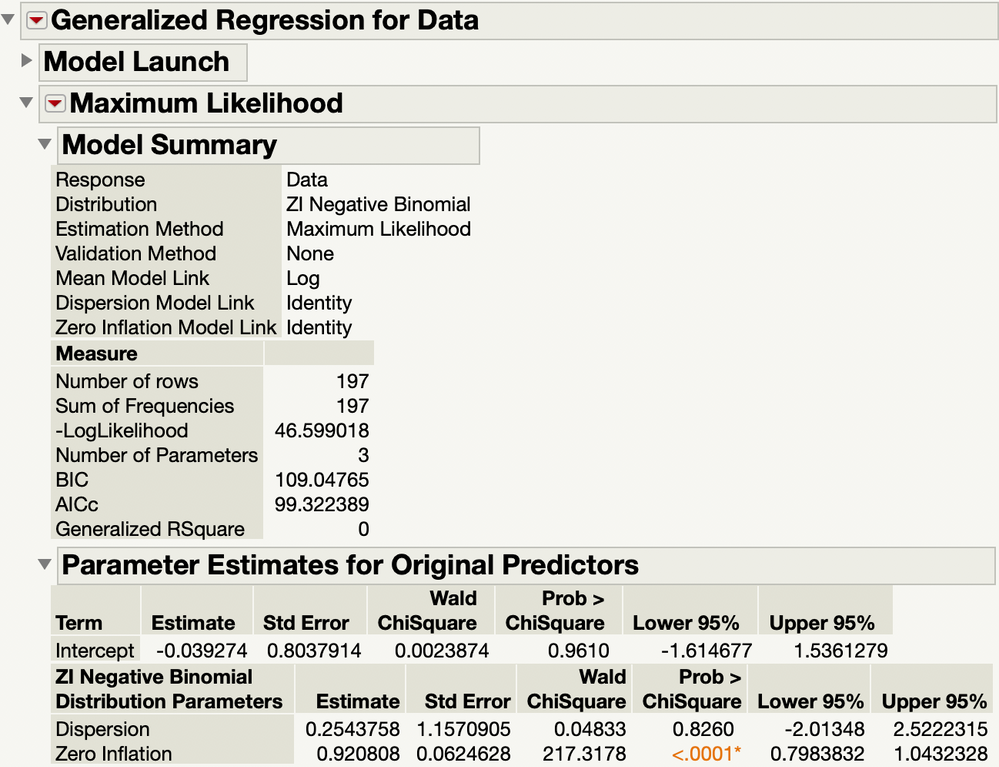
The negative binomial and zero-inflated negative binomial distribution models are available in the JMP Pro Generalized Regression platform. I used an intercept-only linear predictor to get these results:
The AICc suggests that the gamma Poisson distribution is one of the best fits to the data.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Percentile & Goodness-of-fit of Zero Inflated Negative Binomial (ZINB) and Negative Binomial (NB)
I would normally use the Distribution platform to fit such models but the negative binomial distribution is not one of the choices. Here I modelled your data with the gamma Poisson distribution, obtained the goodness-of-fit test statistics, and estimated the 95% quantile:
It seems to do well.
The negative binomial and zero-inflated negative binomial distribution models are available in the JMP Pro Generalized Regression platform. I used an intercept-only linear predictor to get these results:
The AICc suggests that the gamma Poisson distribution is one of the best fits to the data.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Percentile & Goodness-of-fit of Zero Inflated Negative Binomial (ZINB) and Negative Binomial (NB)
And..Can I get more your advice? :)
If the other dataset is matched with ZINB or NB, I need to calculate 95th percentile and 99th percentile from that distribution per the guidance.
(1) Is it possible to get these percentiles from the JMP Pro Generalized Regression platform or other way?
(2) If the dataset is not fitted well with Poisson or NB (maybe i can check it with GammaPoisson), I hv to check goodness of fit for ZINB. Is there a way to check it visually (Q-Q plot) or with other method except AIC or BIC?
Many thanks!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Percentile & Goodness-of-fit of Zero Inflated Negative Binomial (ZINB) and Negative Binomial (NB)
1.) You use the parameter estimates for either the ZINB or NB distribution model to estimate the 95% percentile from the inverse cumulative distribution function.
2.) AIC and BIC are criteria for model selection. They do not assess goodness of fit. JMP does not have a Q-Q plot for these distributions that I know of. They exist in the Distribution platform for the gamma Poisson, though.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Percentile & Goodness-of-fit of Zero Inflated Negative Binomial (ZINB) and Negative Binomial (NB)
Recommended Articles
- © 2026 JMP Statistical Discovery LLC. All Rights Reserved.
- Terms of Use
- Privacy Statement
- Contact Us