- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Discussions
Solve problems, and share tips and tricks with other JMP users.- JMP User Community
- :
- Discussions
- :
- Re: Parallel Line Analysis and Annova
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Parallel Line Analysis and Annova
Dear All,
I have a very easy-difficult question.,that I suppose I have not been able to solve due to my limited ability as a statatician (very sad about it).
This is some kind of a bioassay where 6 replicates are tested at 3 different concns. So there are 18 observations for the Standard and 18 observations for the Test Sample. The aim is to confirm that non-pararalism is not-significant and that non-linearity is not-significant. I assume there is some kind of anvoa available for it.
I have tried every thing, I have no idea how to do. I personally thank and one who can help out. Please.
Best Regards
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Parallel Line Analysis and Annova
First of all, an interaction effect in the response means that the effect of one factor depends on the level of another factor. In this case, if the slope (represents effect of changing log concentration) is different (not parallel) for the curve type, then the slope depends on the sample and there is an interaction effect. on the other hand, if the slope is the same (parallel) for each type, then there is no interaction effect. Most scientists and engineers mistakenly fit a separate model to each sample type and then try to compare them. This way of working is inferior for several reasons.
Second of all, JMP matches the output as far as it goes. The Regression Plot in Fit Least Squares is the same as the plot shown at the end of the PDF under Graphics. The Means and Standard Deviations report in Oneway platform (Y: Response, X: Level, and By: Type) is the same as the summary tables under Observations. The Results section can also be reproduced but it is not clear how they modeled it. It seems that they performed more partitions of the sum of squares than is usual and I cannot reproduce that level. In particular, I cannot achieve the R square values because they included additional factors. I think that it is the Row and Column effect from the Latin Square design. Also, there is no need to perform an ANOVA and a Regression analysis. That distinction is artificial.
Here is what I get from the ANOVA:
Separately, I get the sum of squares for the individual terms: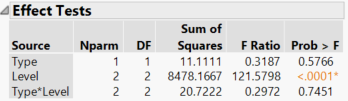
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Parallel Line Analysis and Annova
Your the change in your response appears to be linear so you can use Fit Model for this purpose. (If you had a logistic curve and model, you could use Fit Curve, which has parallelism and equivalence tests built in.) The 'trick' is to use additional terms in the model to test if the slopes are common or unique. This means an interaction effect. So select Analyze > Fit Model. Select your response column and click Y. Select your log concentration column and the sample type column, click Macros and select Full Factorial. Now click Run.
Examine the Effect Tests report. If the interaction term is significant, then the curves are not parallel. If the term is not significant, then the curves are parallel and you can remove this term. Finally, if the term for the sample type is significant, then you have a unique intercept for each type otherwise you can also eliminate this term and use a common intercept. At this point you would have a model with only the intercept and log concentration.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Parallel Line Analysis and Annova
Sir,
I am most greatful to you for your quick response. I see that a part of what I was doing all along was not too far from what is needed.
You mention " If the interaction term is significant, then the curves are not parallel. If the term is not significant, then the curves are parallel and you can remove this term."
What is the meaning of "Interaction", I some how could not find this term ?
Furthermore I have attached the original problem which comes from a PLA3 software calcuation that I am tring to do using JMP. The Anova table generated by this programm is significantly differnet from what I get out of JMP or Minitab. Could you please tell me how to calculate all the factors that PL3 calculates ?
If you could kindly give me some guidance on how the pottention ratio has been calculated ?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Parallel Line Analysis and Annova
First of all, an interaction effect in the response means that the effect of one factor depends on the level of another factor. In this case, if the slope (represents effect of changing log concentration) is different (not parallel) for the curve type, then the slope depends on the sample and there is an interaction effect. on the other hand, if the slope is the same (parallel) for each type, then there is no interaction effect. Most scientists and engineers mistakenly fit a separate model to each sample type and then try to compare them. This way of working is inferior for several reasons.
Second of all, JMP matches the output as far as it goes. The Regression Plot in Fit Least Squares is the same as the plot shown at the end of the PDF under Graphics. The Means and Standard Deviations report in Oneway platform (Y: Response, X: Level, and By: Type) is the same as the summary tables under Observations. The Results section can also be reproduced but it is not clear how they modeled it. It seems that they performed more partitions of the sum of squares than is usual and I cannot reproduce that level. In particular, I cannot achieve the R square values because they included additional factors. I think that it is the Row and Column effect from the Latin Square design. Also, there is no need to perform an ANOVA and a Regression analysis. That distinction is artificial.
Here is what I get from the ANOVA:
Separately, I get the sum of squares for the individual terms:
Recommended Articles
- © 2026 JMP Statistical Discovery LLC. All Rights Reserved.
- Terms of Use
- Privacy Statement
- Contact Us