OLS Variable importance , interaction terms and some unexpected errors

[#1]

Hello

I am doing a simple OLS regression with continuous DV and IV. I enabled the prediction profiler and chose assess variable importance and got the table with main and total effects and their std. errors. If I add an interaction term to my OLS model, the prediction profile is throwing an error " variable importance requires at least two rows in the data table). Not sure if it is due to interaction term or some other issue. 

On a related note, is the prediction profiler and relative variable importance for OLS models capable of handling interaction terms? Is there anyway to see the importance of interaction terms and the main terms?  By looking at the main and total effect (with interaction terms and without interaction terms) of the variable importance table , can the net change be attributable to interaction?  

using JMP 15.3 pro, windows 10

[#2]

The profiles are based on the whole model, including any non-linear terms. The profile for one variable simply fixes the other variables at their current value. So the sampling of variable values is used with the entire model:

This model includes terms for all three interaction effects.

[#3]

@Mark_Bailey thanks for response and proviidng the example

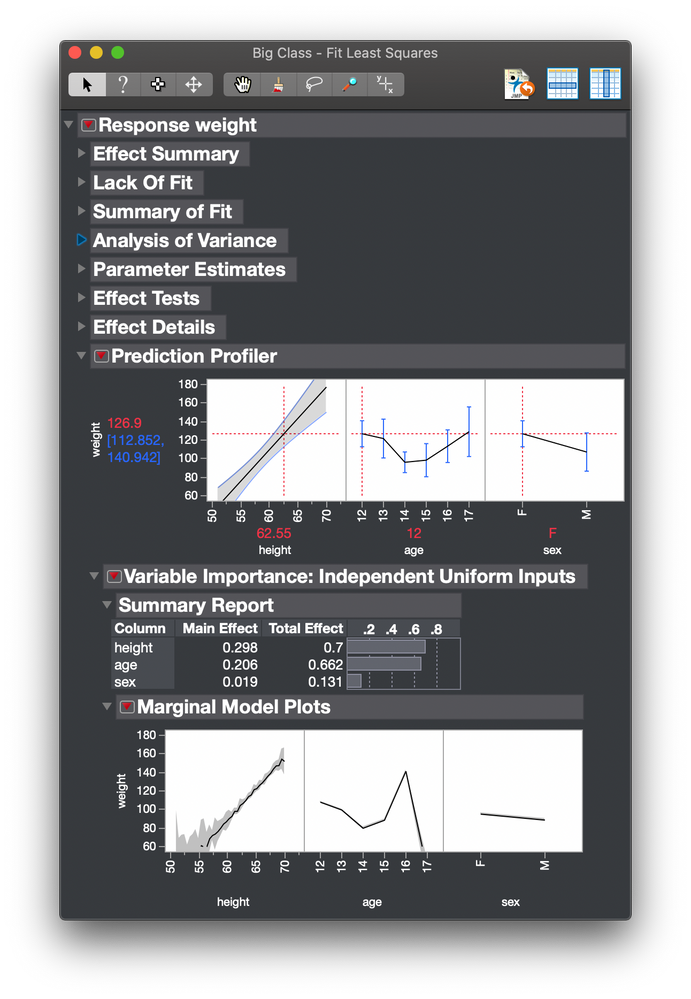
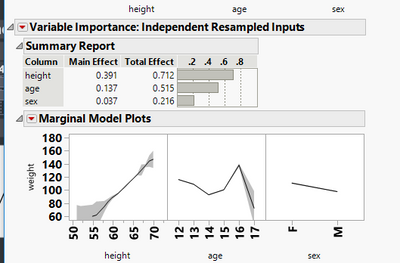
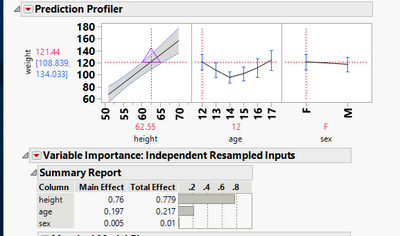
I replicated the same model and provided screenshot of 2 version, one which has only the main effects and the second which has all 3 interactions and main terms.The main effect of height in the no-interactions model is 0.76, whereas in the factorial to degree interaction model, it is 0.391.How to read more into these two numbers? Basically I am trying to assess the rel importance of height alone and height*weight and so on. 

1)This difference ~0.36 is due to the interaction of height with other terms as well as the other terms 

2) 0.76 includes main effect of height and interactions?

3) Are interaction terms implicitly treated as another independent variable irrespective of whether the model explicitly includes main and interaction effects?

factorial to degree main and interactions

Only main effects and no interaction terms

[#4]

The Total Effect is defined as an index that is directly proportional to the variability in the predicted response for some given variation in the factor or predictor. This index reflects the relative contribution of that factor both alone and in combination with other factors.

So, if I select the first-order model, the Total Effect of height, age, and sex is 0.779, 0.217, and 0.01, respectively. On the other hand, if I select the model with first-order terms and cross terms, the Total Effect of height, age, and sex is 0.712, 0.515, and 0.216, respectively. I would not expect the importance of any one variable to remain the same across different models. The change in an index across models is not important.

The profilers are provided for the exploitation stage of modeling, which follows the selection stage. We might monitor the change in AICc across different models during the selection stage. AICc would not be useful in a prior or subsequent stage. Similarly, the total effect index is useful during exploitation of the selected model, not in a prior stage.

You should not use this feature to select one model over other candidate models. You should use this feature to explore and understand the selected model. So looking at changes in this index across different models using the same factors is not meaningful.

Please see Help > JMP Documentation Library > Profilers > Chapter 3: Profiler. There is an entire section in this chapter devoted to explaining the Assess Variable Importance feature. The end of this chapter includes a section with the statistical details, including those for the calculation of the various importance indices.

[#5]

One further comment. You said, "How to read more into these two numbers? Basically I am trying to assess the rel importance of height alone and height*weight and so on." One interpretation of this statement is some mis-understanding about the linear statistical model. It is simply a linear combination of terms, each with a single parameter as a coefficient. There is no such thing as a height^2 effect, for example. There is simply a height effect that might require several terms to be adequately modeled: height, height^2, height*age, and so on. The height effect is represented by the combination of all these terms. It doesn't make sense to talk about sub-effects. They are merely an artifact of the linear model. No such terms exist in other models that we might use, such as recursive partition, neural network, or Gaussian process.

Another interpretation of this statement is that you want to know the benefit of including higher order terms to represent the effect of any given factor. You could answer that question during the previous selection stage using inference about a term (e.g., t-ratio or F-ratio) or the AICc for the model.

Please do not mis-interpret me. I am not saying that what you are doing is wrong, I am saying that you might be using this index in a way that it was not intended to be used.