Nominal Logistic Regression question re: the Save Probability Formula

[#1]

I am trying to develop a model to predict whether a tree will live or die over a 25 year period given some environmental attributes associated with each tree.  I ran the Nominal Logistic Regression model, which showed that the Prob>ChiSq for each attribute was < 0.0001, which would seem to suggest that the environmental attributes could be used as a good predictor.  Wanting to see how good of a prediction they were I selected the Save Probability Formula option.  This added several columns to the table including the final column, which provided a prediction (Most Likely), Live or Dead.  The predictions were terrible.  The model predicted a total of 140 trees would be alive after 25 years, when in fact the number was about 1000.  Not only that, but many of the 140 predicted live trees in fact had died.  So, my question is, why were the predictions not even close to the actual Live/Dead data? 

[#2]

You can have a statistically significant model that does a poor job of prediction. Statistical significance is telling you that those significant terms HELP to explain the response, but does not guarantee a good fit.

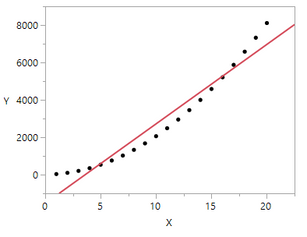
For example, with a continuous response, look at this picture:

The model is statistically significant, but clearly would not predict well. 

Determining why the model does not fit well can be difficult with a nominal logistic regression. A few things that can help you determine predictive ability rather than "eyeballing" the table.

* You can ask for the ROC curve. The Area Under the Curve (AUC) is an indication of predictive ability. An AUC of 0.5 is the "baseline". This is like using a coin to determine if the tree will live or not. Anything above 0.5 starts providing evidence of predictive ability. AUC above 0.7 is starting to get to decent predictive ability. Above 0.9 is fantastic.

* You can also ask for the confusion matrix. This is a table of observed results versus predicted results. This table is essentially what you were considering by saving the prediction formula. This can help you determine where your model is starting to have trouble. Is it having trouble classifying trees that are dead? Or is it having trouble with just trees that are alive? Or both?

Don't forget to assess the data that the model was built on. How "balanced" is the data between live and dead trees? For example, if there are only 1% of the trees being dead, a great predictive model would be to say that all trees are alive. 99% accuracy! Not very helpful though. For this reason having a response that is pretty close to balanced can be helpful.

Was the model only containing main effects? Would interactions help? What about quadratic terms? Is the data "rich" enough to support a model with these higher order terms (this is a great question if those higher-order terms are already in the model, too!).

You could also try a different modeling technique. Perhaps a Partition or tree model would be a good thing to try. There are other tools, too.

I'm sure others can add more things to help, but this is where your fun REALLY starts! Best of luck!

[#3]

Dan, I ran the Confusion Matrix and it showed that the model was doing decently predicting the dead trees, correctly predicting 3/4 of them as dead.  But it was doing terrible predicting the live trees, predicting 63% of them as dead.  The distribution of live and dead trees is about 45%,55%, so pretty well balanced.  Why would the model do a decent job predicting the dead trees but not the live trees?--Mark

[#4]

Dan's comments are relevant, but one thing you should check is that the predictions (alive or dead) are based upon a 50% threshold for classifying the trees.  If the AUC (from the ROC curve) is high (closer to 1 than to 0.5), then it is likely that using a different threshold value for classifying the trees will result in better predictions.  This is especially true if the data is very unbalanced (i.e., if there are very few dead trees, then it is likely that most of the probabilities estimated from the logistic regression will be quite low, resulting in the default prediction of "not dead").  There is a nice add-in you can use (just search for it) that will produce confusion matrices for alternative cut-off classification probabilities.

On other thing struck me about your description.  It sound like this is censored data - after 25 years, the trees that are alive are probably not all of the same health.  If environmental conditions contribute to tree death, then the surviving trees are probably also affected, but not dead yet.  If you have a measure of the time at which the trees died, you can try a survival analysis, where the dependent variable is the time of death and censored data can be used in the analysis.

[#5]

Dale may be right. But assuming that the cutoffs are not playing much of a role, your model is biased towards predicting Dead. That seems to indicate that there is something that is likely missing from your model that is indicative of a live tree. I can't tell you what that is. I also am not completely confident that my statement is correct. This is where looking at the data and having knowledge of the field is necessary.

[#6]

Dan, thanks for getting back to me. First, thanks very much for the ROC and confusion matrix (odd name) suggestions. They were very helpful. My best model produced an ROC of 0.798, which was pretty decent. Of course this was predicting the overall number of live and dead trees 25 years later, not the dead or alive predictions for individual trees, which as described below came out around 63%. The 2020 trees were about 1/3 live and 2/3 dead over the 25 year period. While not 50/50 balanced, still not too skewed. I took Dale's suggestion and played around adjusting the prediction threshold (set at 0.5) used to classify/predict individual trees as live or dead. By adjusting the threshold to 0.5+0.284, I was able to get the correct prediction percentages for Live and Dead trees balanced at 63%, though the number of correct predictions actually declined slightly (4%) from the original highly skewed toward dead predictions resulting from a 0.5 prediction threshold. You might think the 67% tree mortality rate over 25 years was really high. It would be under normal conditions. The high mortality rate was because the area where I was tracking the roughly 10,000 trees was burned 8 times over the 25 year period. --Mark

[#7]

How would I set up a table to calculate mean or median survival times for seven groups of trees over a 25 year period.  Nearly 10,000 trees are involved and I don't want to enter the time to death for each tree.  What I do have for each group is the number of trees still alive for each of the 25 time periods as well as the number of trees that died in each time period.  All the groups have trees still alive after 25 years (some few, some a lot), so I will have to incorporate censoring into the table as well.  Is it possible to create a survival analysis table using the above data?  I hope so since the prospect of having to enter the survival time for each of the 10,000 trees is pretty dim.  Thanks so much for the prior comments and suggestions.  They have been very helpful!--Mark

[#8]

Ok, I think I've figured out how to enter data with a frequency column that enables me to run the survival analysis.  After selecting the 'compare groups' option the results show the mortality curve and also the mean survival times for the two groups, the latter which is what I was looking for.  When I select the 'life distribution' option, the results show the individual life survival curves for each group in separate graphs.  Is there a way to get the survival curves for both groups on a single graph? (I know I can easily show the both survival curves on a single graph by copying the data into Excel, but it seems like I should be able to do this on JMP as well.)  Any suggestions?  FYI I've included the data table.  Is there a way to get the the results to show the survival curves on a single graph?  Thanks for the suggestions.--Mark

[#9]

The data table you attached does not have any data on the number of trees alive and dead in each time period (I'm not sure what "Count" represents, but it doesn't account for 10,000 trees).  So, I can't attempt to get that visual from your data.  But if you have a survival graph for each group separately and want them on the same graph, you can use "copy graph" to copy and paste one graph into the other and they should be overlaid.  There may well be a way to get the survival analysis to do that automatically, but I can't tell what your data is like from the table you attached.

[#10]

Sorry, Dale.  The Count column was the number of trees that died during that time period.  The reason Count doesn't add up to near 10,000 is because these were data from just one of the three burn units.  I did find out how to get the survival curves for all 7 groups on one graph.  After selecting Reliability and Survival then select Survival (instead of Life Distribution).  This will put the survival curves for all 7 groups on one graph.  The Survival optin expects that the data column (Count in this case) was listing the number of units that died, or failed, in each time period.  Very nifty.