- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Discussions
Solve problems, and share tips and tricks with other JMP users.- JMP User Community
- :
- Discussions
- :
- Re: Need some scripting help - Linear fit where slope is the largest
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Need some scripting help - Linear fit where slope is the largest
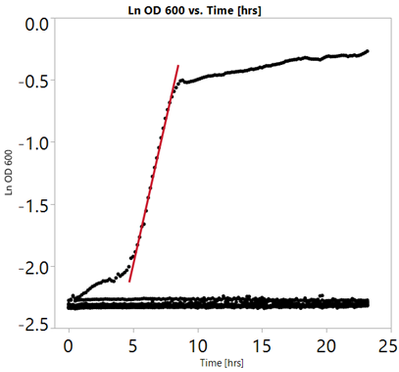
I am studying the growth of a bacterium in liquid growth medium in the wells of a 96-well plate. I want to get the maximum growth rate, which is the slope of a straight line in the exponential growth phase, as below:
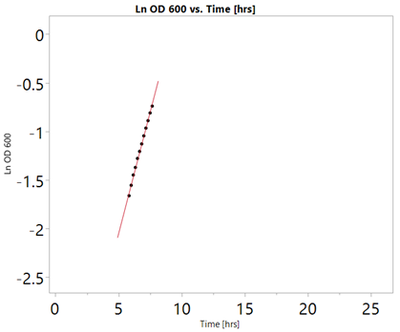
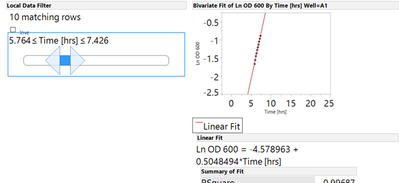
What I need to do is to cut the data from both directions so that the line fits to the 10 data points which have the largest slope.
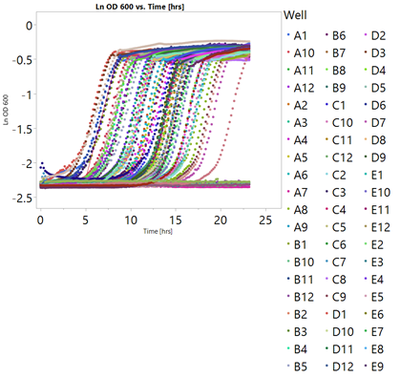
Each of my data tables has 96 of these curves indicated with a letter-number designation (“Well”).
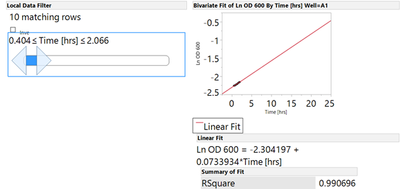
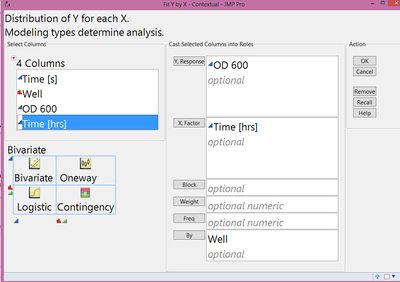
The y-axis data is natural log transformed “(Ln OD 600”) and the x-axis data is in hours (“Time [hrs]”). Currently I have written a script that uses the Fit Y by X platform, puts “Ln OD 600” in the Y response, “Time [hrs]” in the X factor, and “Well” in the By-box. So I get a report with 96 different graphs, to each graph it fits a line and opens a local data filter using “Time [hrs]” and cuts it to 10 data points/matching rows.
Then I manually have to slide that filter/slider across time to find the the largest slope of the line. I have a couple hundred of the data files so it takes a ton of time to do!
What I am trying to do is write a script that would automatically move the slider across time and to find the largest slope of the line. Unfortunately scripting and coding is not one of my skill-sets so I am stumped. I have attached my JSL script as of right now. Thank you for any help or thoughts!
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Need some scripting help - Linear fit where slope is the largest
Try this script on your data and see if it is closer to what you want:
Names Default To Here( 1 );
// open the data table
dt = Current Data Table();
Summarize( dt, Well List = by( :Well ) );
dt << color by column(:Well);
// Pass through each Well's data and find the best 10 contiguous points
// with the best slope
For( i = 1, i <= N Items( Well List ), i++,
// Setup the Lists to contain the determined 10 data points with highest slope
dt << select where( :Well == Well List[i] );
bestbeta = 0;
startrow = 0;
yall = :Ln OD 600[dt << get selected rows];
xall = :Time[dt << get selected rows];
For( k = 1, k <= N Rows( xall ) - 10, k++,
x = xall[k :: k + 9];
x = J( N Row( x ), 1, 1 ) || x;
y = yall[k :: k + 9];
// regression calculations
xpxi = Inverse( x` * x );
beta = xpxi * x` * y;
If( Abs( beta[2] ) > bestbeta,
bestbeta = Abs( beta[2] );
startrow = (dt<<get selected rows)[k];
);
);
For( k = Min( dt << get selected rows ), k <= Max( dt << get selected rows ), k++,
If( startrow<= k <= startrow + 9,
Row State( k ) = Excluded State( 0 ),Row State( k ) = Excluded State( 1 )
);
);
);
// Create the graphical output
Bivariate( Y( :Ln OD 600 ), X( :Time ), Group By( :Well ), Fit Line( 1 ) );
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Need some scripting help - Linear fit where slope is the largest
Here is a script that I believe will do what you want. It is setup as an example using the JMP Sample data table called Big Class. However, if you just point the script to the data table you want to run against, and change the Y Var = "age"; to the Y column you want to run against, you should get what you want. There are 2 assumptions with the script.....the first is that all numeric, continuous columns in the data table are to be analyzed, and the second assumption is that the data in the columns are ordered by the X variable. If this is not the case, the script can be modified to handle that situation. It will just add more processing time I changed the script to do the sorting.
Names Default To Here( 1 );
// open the data table
dt = Open( "$SAMPLE_DATA/Big Class.jmp" );
Y Var = "age";
// get data into matrices
ColList = dt << get column names( continuous, string );
// Get rid of the Y variable from the list
ColList = Remove( ColList, Contains( ColList, Y Var ), 1 );
// Setup the Lists to contain the determined 10 data points with highest slope
Best Data = {};
Best Ys = {};
Column Names = {};
bestbeta = 0;
startrow = 0;
// Loop across the columns
For( i = 1, i <= N Items( ColList ), i++,
// Sort the data to insure the data is in ascending X
dt << sort( by( Collist[i] ), order( ascending ), replace table( 1 ) );
yall = Column( Y Var ) << getValues;
xall = (Column( dt, collist[i] ) << getValues);
For( k = 1, k <= N Rows( xall ) - 10, k++,
x = xall[k :: k + 9];
x = J( N Row( x ), 1, 1 ) || x;
y = yall[k :: k + 9];
// regression calculations
xpxi = Inverse( x` * x );
beta = xpxi * x` * y;
If( Abs( beta[2] ) > bestbeta,
bestbeta = Abs( beta[2] );
startrow = k;
);
);
Best Data = Best Data || As List( xall[startrow :: startrow + 9] );
Best Ys = Best Ys || As List( yall[startrow :: startrow + 9] );
For( k = 1, k <= 10, k++,
Insert Into( Column Names, ColList[i] )
);
);
// Create the new data table with the best 10 points for all columns
dttogether = New Table( "The Results",
New Column( "Column Name", character, values( Column Names ) ),
New Column( "Y", values( Best Ys ) ),
New Column( "Data", values( Best Data ) )
);
// Create the graphical output
dttogether << color by column( :column name );
Bivariate( Y( :Y ), X( :Data ), Group By( :Column Name ), Fit Line( 1 ) );
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Need some scripting help - Linear fit where slope is the largest
Jim,
Thank you for the reply and thoughts! I was able to alter the script to apply to my table and run it. However, I actually need for the line to be fit for each curve, when each curve is plotted with time as the x-axis. Then I need to select 10 contiguous points (contiguous according to time) which produce the largest slope. My apologies if I wasn't clear about that. Basically if there are 10 minutes between each point, I am looking for the 100-min period which has the largest slope of the line.
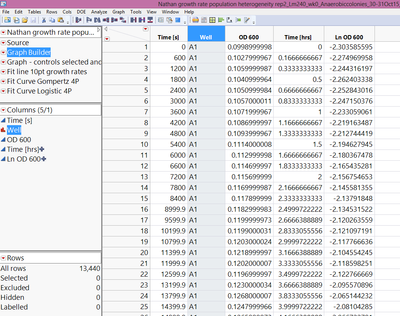
Here is a snap shot of my data sheets. Basically in the "Well" column there are 96 letter-number combination identifiers. Each identifier has 140 or so rows. Then I plot the "Time [hrs]" on the x and the "OD 600" on the y, "Well" in the By box. Does that help?
Here is the dialog box:
Thank you very much for the help!
~Nathan
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Need some scripting help - Linear fit where slope is the largest
My mistake in thinking each of the different Well values were in different columns. It won't be a major project to modify the script to meet your needs. I will not be able to get to it until tomorrow afternoon, but I will get it to you then.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Need some scripting help - Linear fit where slope is the largest
Jim,
Wonderful, thank you! I probably did not make that clear. This is my first foray into scripting. I appreciate the help,
Nathan
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Need some scripting help - Linear fit where slope is the largest
Try this script on your data and see if it is closer to what you want:
Names Default To Here( 1 );
// open the data table
dt = Current Data Table();
Summarize( dt, Well List = by( :Well ) );
dt << color by column(:Well);
// Pass through each Well's data and find the best 10 contiguous points
// with the best slope
For( i = 1, i <= N Items( Well List ), i++,
// Setup the Lists to contain the determined 10 data points with highest slope
dt << select where( :Well == Well List[i] );
bestbeta = 0;
startrow = 0;
yall = :Ln OD 600[dt << get selected rows];
xall = :Time[dt << get selected rows];
For( k = 1, k <= N Rows( xall ) - 10, k++,
x = xall[k :: k + 9];
x = J( N Row( x ), 1, 1 ) || x;
y = yall[k :: k + 9];
// regression calculations
xpxi = Inverse( x` * x );
beta = xpxi * x` * y;
If( Abs( beta[2] ) > bestbeta,
bestbeta = Abs( beta[2] );
startrow = (dt<<get selected rows)[k];
);
);
For( k = Min( dt << get selected rows ), k <= Max( dt << get selected rows ), k++,
If( startrow<= k <= startrow + 9,
Row State( k ) = Excluded State( 0 ),Row State( k ) = Excluded State( 1 )
);
);
);
// Create the graphical output
Bivariate( Y( :Ln OD 600 ), X( :Time ), Group By( :Well ), Fit Line( 1 ) );
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Need some scripting help - Linear fit where slope is the largest
Jim,
This is wonderful! I have run it on 1 complete set of data and the line slopes calculated by the script are correlated to the slopes calculated by hand with a R-squared of 0.98. I suspect the little bit of variation is due to the error involved in calculating them by hand. I will do some more with it, but this looks like exactly what I needed! I will post again once I have run it on some of my already analyzed data files on its performance.
Thank you so very much for the help,
Nathan
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Need some scripting help - Linear fit where slope is the largest
Hi Jim -
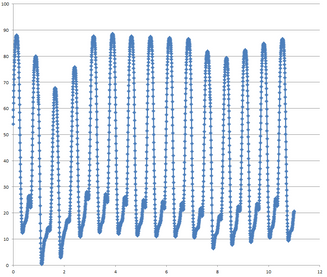
How would you modify the script to find the greatest slope of the data exemplified in the above graph over the course of the range? I tried to modify your script but it did not properly exclude any rows. It is in the same format as the OP. Each "well" has a similar waveform.
Thanks,
Drew
Recommended Articles
- © 2026 JMP Statistical Discovery LLC. All Rights Reserved.
- Terms of Use
- Privacy Statement
- Contact Us