- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Discussions
Solve problems, and share tips and tricks with other JMP users.- JMP User Community
- :
- Discussions
- :
- Concordance analysis with continous variable
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Concordance analysis with continous variable
Hello,
I am trying to solve the following statistical problem in jmp:
1. I got a gold standard fixed variable y (for example: y = 100)
2. I got three data sets x1,x2,x3: (for example x1=92;94;99 / x2=92;94;99;101;103 / x3=92;94;99;101;103;107;100;99;100)
please note: the data sets have similar data, but the number of data points are different. all variables are continuous.
I am looking for with a statistical test or function, to evaluate which dataset x1, x2 or x3 has the closest mean AND the lowest SD to match the gold standard y ? - please note: the gold standard y has no sd, just a fixed value. Looking at ther samples for concordance analysis I just could do this was nominal variables; mine are ordinal or continous.
Any advice much appreciated. Many thanks, Marc
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Concordance analysis with continous variable
I understand your use of the word 'concordance' here but that word is also a statistical term that refers to measures of agreement among categorical variables.
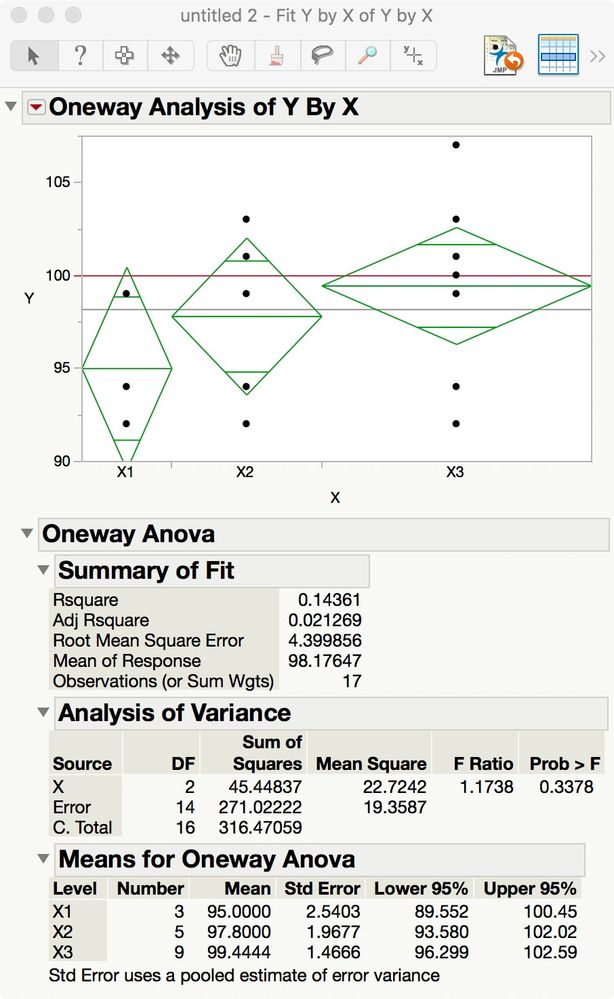
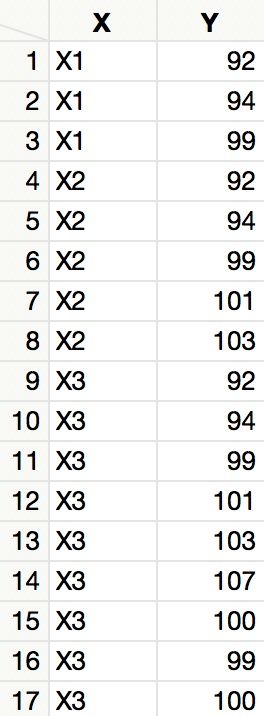
I recommend using confidence interval estimates of the mean. The 'gold standard' is your null hypothesis H0: mean = 100) and therefore your alternative hypothesis is that the opposite (H1: mean not = 100). You compare the intervals to the gold standard and to each other using Analyze > Fit Y by X (Oneway platform). Here is your example in a data table laid out for Oneway:
Here is the Oneway platform with a reference line for the gold standard and the results for ANOVA:
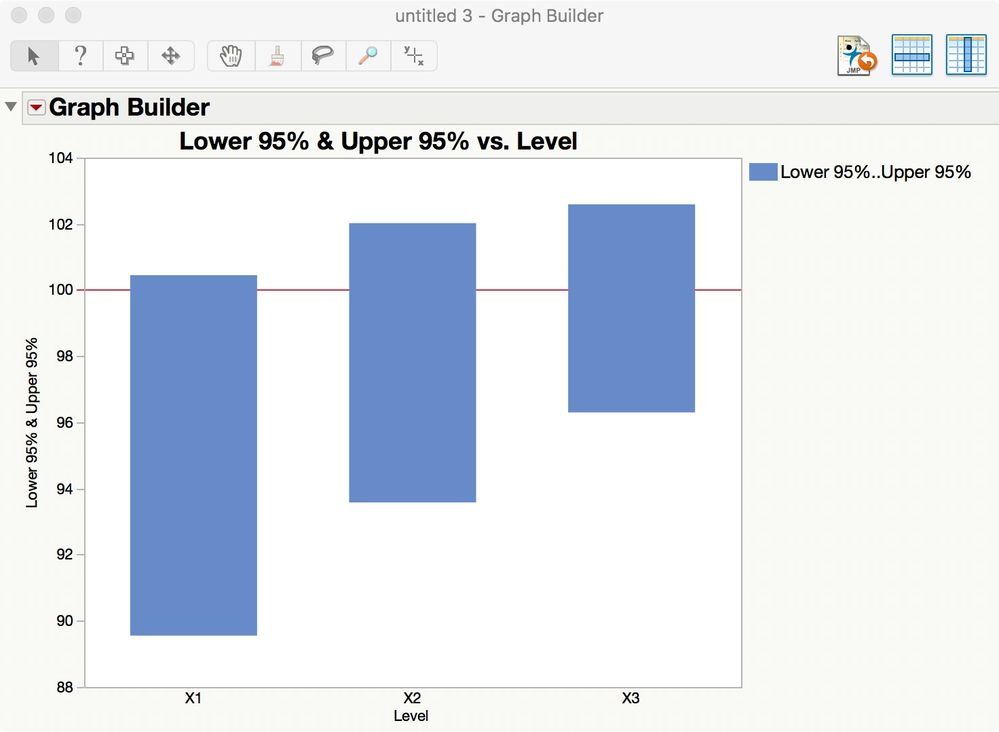
Now you compare the confidence interval for each sample. You can plot them in Graph Builder, too. Right-click on the Means for Oneway Anova table and select Make Into Data Table. It might look like this:
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Concordance analysis with continous variable
Many thanks @Mark_Bailey !
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Concordance analysis with continous variable
I understand your use of the word 'concordance' here but that word is also a statistical term that refers to measures of agreement among categorical variables.
I recommend using confidence interval estimates of the mean. The 'gold standard' is your null hypothesis H0: mean = 100) and therefore your alternative hypothesis is that the opposite (H1: mean not = 100). You compare the intervals to the gold standard and to each other using Analyze > Fit Y by X (Oneway platform). Here is your example in a data table laid out for Oneway:

Here is the Oneway platform with a reference line for the gold standard and the results for ANOVA:
Now you compare the confidence interval for each sample. You can plot them in Graph Builder, too. Right-click on the Means for Oneway Anova table and select Make Into Data Table. It might look like this:
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Concordance analysis with continous variable
Many thanks @Mark_Bailey !
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Concordance analysis with continous variable
You need to change the "Accepted Solution" from your response to Mark Bailey's response. The marking of an "Accepted Solution" is not intended to just indicate that a solution to a Discussion Question has been found, but it need to point to the response that has the actual solution
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Concordance analysis with continous variable
hi
do you have any software for solve concordance analysis prpblems?
Recommended Articles
- © 2026 JMP Statistical Discovery LLC. All Rights Reserved.
- Terms of Use
- Privacy Statement
- Contact Us