Need some advice regarding parallelism test.

[#1]

I am using JMP version 16.1 and working on comparing a nonlinear standard curve (ID- STD) against 3 other nonlinear curves (ID- Set A, B, C) to see if they are similar.

What I did was plotting the 4 curves using analyze>specialized model>nonlinear set up as attached. After that I select logistic 4P and perform Parallelism test and Equivalence test. The p-value obtained is 0.0056 which is below 0.05 and all stats in equivalence test does not match the STD curve. Thus, I am right to say these 4 curves are not comparable?

However, I did a normalization of the results and did the same test but this time round I select logistic 2P for the curve and I got a P-value of 0.6794 which shows 4 curves are comparable but the stats in equivalence test does not match the STD curve. Thus, I am quite lost of the data I have and not too sure how to interpret it. 

Any advice would be great. Thank you.

 I have attached the data I use for the study.

[#2]

First of all, the choice of the Logistic 4P model is overly optimistic. There is only the lower asymptote and no inflection point, so you won't have a good estimate of the upper asymptote for comparison. This situation also leads to unstable estimates for all the parameters.

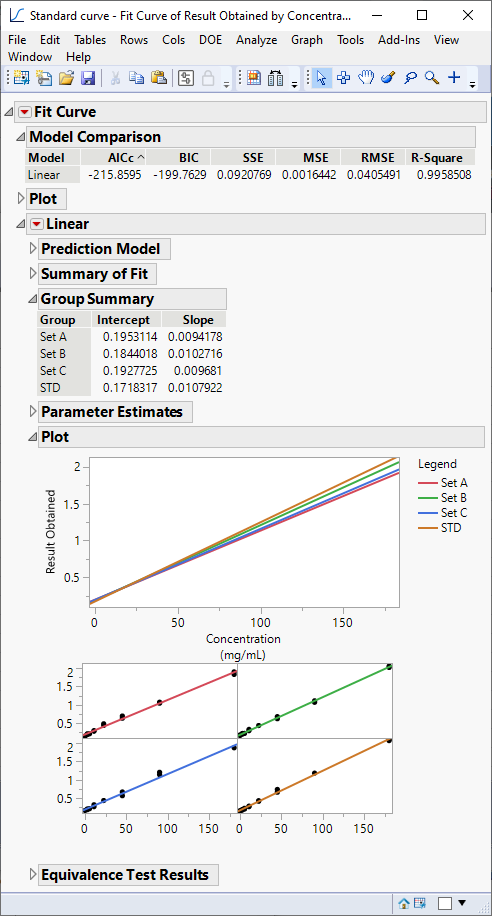
Second, why use a complicated non-linear model for this data? A plot of result obtained versus concentration appears to be linear. The Fit Curve platform can fit such models and assess them for parallelism, too.

[#3]

 Hi Mark, thank you so much for your advice. I guess I need to extend the standard curve to find out the upper asymptote.

The reason for the non-linear curve is recommended by the Elisa assay kit as it stated that using linear regression analysis to interpolate values for samples can lead to significant inaccuracies.