- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Discussions
Solve problems, and share tips and tricks with other JMP users.- JMP User Community
- :
- Discussions
- :
- Multinominal logistic regression plot intepretation
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Multinominal logistic regression plot intepretation
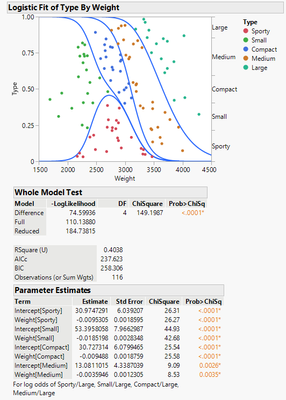
Below are two plots for logistic regression with the one on the left for ordinal response and the one on the right for the multinominal response. They both have k-1 curves with k being the number of levels but are both of them accumulative in terms of probability interpretation? In other words, the probability at a certain X value (car weight) on each curve is the overall probability for the car size at that level and the all the levels below that? If both the ordinal plots and nominal plots are interpreted the same way to get the probability for certain car type at certain weight value, why the two plots look very differently? is it simply because the type of response with one being ordinal and the other nominal? I had an impression that JMP recommend to use ordinal logistic regression even for nominal response since it is easier to analyze and interpret. However, if the results will be very different like shown here, one should not use ordinal logistic regression for nominal response. Any comments will be appreciated. Thanks.
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Multinominal logistic regression plot intepretation
The difference between the logistic regression model for a nominal response and an ordinal response is the odds in the logit transformed response. (Both are multinomial responses.) The ordinal response uses the 'cumulative logit' and the nominal uses the 'generalized logit' as the response. Assume that the response variable Y has K levels. There will be K-1 logits, since the probabilities are constrained to sum to 1. The two types of logits are the cumulative logit:
and the generalized logit:
The two types of logits further use different linear predictors for each level of the response. The ordinal logistic regression takes advantage of the cumulative logit and estimates a different intercept (constant) term for each level but uses common parameters for the predictor terms for all levels. On the other hand, the nominal logistic regression uses a unique set of parameters for each logit. You can verify this claim by examining the Parameter Estimates table in the Logistic platform.
Answers to your questions:
- Yes, the back-transformation of the fitted log odds to the fitted probability maintains that each logistic curve represents probability of the given level level compared to the previous level. So the probability for level 1 is the difference between the first logistic curve and the horizontal axis, the probability for level 2 is the difference between the second logistic curve and the first logistic curve, and so on.
- The plots look different because the logit and the linear predictor (i.e., your model) are different.
- Yes, it is simply the difference between an ordinal and a nominal response, and the change that forces in the logits and the linear predictors for each level.
- I do not know where you got the impression that ordinal logistic regression is preferred over nominal logistic regression. The best model is the one that fits the data best based on minimal bias and variance (e.g., minimum AICc).
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Multinominal logistic regression plot intepretation
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Multinominal logistic regression plot intepretation
The difference between the logistic regression model for a nominal response and an ordinal response is the odds in the logit transformed response. (Both are multinomial responses.) The ordinal response uses the 'cumulative logit' and the nominal uses the 'generalized logit' as the response. Assume that the response variable Y has K levels. There will be K-1 logits, since the probabilities are constrained to sum to 1. The two types of logits are the cumulative logit:
and the generalized logit:
The two types of logits further use different linear predictors for each level of the response. The ordinal logistic regression takes advantage of the cumulative logit and estimates a different intercept (constant) term for each level but uses common parameters for the predictor terms for all levels. On the other hand, the nominal logistic regression uses a unique set of parameters for each logit. You can verify this claim by examining the Parameter Estimates table in the Logistic platform.
Answers to your questions:
- Yes, the back-transformation of the fitted log odds to the fitted probability maintains that each logistic curve represents probability of the given level level compared to the previous level. So the probability for level 1 is the difference between the first logistic curve and the horizontal axis, the probability for level 2 is the difference between the second logistic curve and the first logistic curve, and so on.
- The plots look different because the logit and the linear predictor (i.e., your model) are different.
- Yes, it is simply the difference between an ordinal and a nominal response, and the change that forces in the logits and the linear predictors for each level.
- I do not know where you got the impression that ordinal logistic regression is preferred over nominal logistic regression. The best model is the one that fits the data best based on minimal bias and variance (e.g., minimum AICc).
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Multinominal logistic regression plot intepretation
Thank you for the detailed explanation. Since both nominal and ordinal curves are cumulative, the ordinal plot indicates that a car having a weight of 2000 lbs will have more than 70% of probability to be a sporty car but the nominal plot indicates that a car having a weight of 2000 lbs will have close to 100% of probability to be a small car (the sport car curve just slightly above 0 at x of 2000 lbs on the nominal plot). Someone may argue the response type can be nominal or ordinal for this example but the predictions are so different at least for that specific car weight at 2000 lbs. I guess I should go with the nominal model, which higher R^2 and slightly lower misclassification rate.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Multinominal logistic regression plot intepretation
Hi @JMP38401 ,
The analyses are showing the same thing, but correctly "categorize" the Type of vehicle by weight, but do it in different ways because one is considered an ordered list of weight values, whereas the other is considered any set of continuous weight values -- not necessarily ordered by their values. You'll also notice that the parameter estimates are different for the different fits because of this.
Both have k-1 curves as you point out, but they have k regions that are bounded by the curves. It might help if you color the rows based on the vehicle type: Rows > Color or Mark by Column > select Type. Then when you view the fits, you can see how the logistic fit has essentially partitioned the data, see the below examples from the Car Physical Data.jmp file. Treating weight as ordinal is easier to interpret in the fit model graph, and provides a marginally better fit. After saving the prediction formulas from each fit to the data table, you can then use the "Most Likely Type" as the X and Type as Y in the Fit Model platform. If you look at Fit Details, you'll see the fit statistics for weight being ordinal is slightly better.
My understanding of the fit is that each level of the response (minus one level) gets it's own probability curve based on a linear fit function that it then converts to a cumulative probability using the logist function. It then calculates the probability for each type by subtracting off one cumulative value from the next. The final level is just the remainder such that all the probabilities need to sum to 1. This would be if the X factor is ordinal. If it's just continuous, then it treats it different and performs the calculations for the probability functions differently. In either case, it determines the Most Likely Type by evaluating a If Max() function on the probability for types. Whichever one of those has the largest value, it assigns that row a most likely vehicle type. Both fits aren't that good as they each have about a 55% misclassification rate, which is really high.
Hope this helps!,
DS
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Multinominal logistic regression plot intepretation
Recommended Articles
- © 2026 JMP Statistical Discovery LLC. All Rights Reserved.
- Terms of Use
- Privacy Statement
- Contact Us