Model reduction

[#1]

Hello,

According to the JMP learning model for DOE analysis, non-significant terms in the model can be removed, starting with the non-significant higher order interactions (= model reduction).

However, is it really that simple? Are there other things to take into considerations before removing non-significant terms? Does removing a non-significant term necessarily meant that this factor has no/minor effect on your output/response variable?

Additionally, does model reduction also apply for REML/mixed models?

Thank you for any clarification on this matter.

Sara

[#2]

It's not that simple. Removing model terms or not ranks right up there with the ongoing discussion of use/abuse/misuse of p-values. In fact, to me, it's kind of two sides of the same coin.

Having said this, however, I'm safe in saying removing a model term does not mean a factor(s) involved in the parameter estimate has '...no/minor effect on your output/response variable?' It just means over THAT particular inference space you are deciding to not include the term in the model. That decision is worlds away from declaring to God and all who will listen there is 'no /minor effect.' Maybe the levels you choose (if modeling a designed experiment) were too narrow for a signal to rise above the noise. Maybe the noise(s) in the inference space are overwhelming the effect of the factor(s). And don't get me started on 'p-value' interpretation...all terms are 'significant' at some p-value. Who picks that significance value? By what criteria?

And IMO same can be said for just about any modeling method (REML/mixed and others) I can think of. 

[#3]

Hi P_Bartell,

I understand the complexity of that matter. However, my reasoning is that at some point you want to be able to make inferences based on the results of the DOE you have performed. Otherwise, what is the purpose of performing it... So from a practical point of view, what do you do with the non-significant terms?

Thank you

Sara

[#4]

Pete is, of course, correct and wise in his advice.  Particularly the issue of inference space.  When you ran your experiment, how representative was the noise in the study?  How was noise handled in the study? (e.g., did you restrict, block, repeat. replicate, partition with split-plots)?  Is the estimate if MSE reasonable and does it represent the true random error?  If not is not, then statistical significance is meaningless.  Remember, statistical significance is a conditional statement!

When doing model reduction, here are things you should consider:

1. Practical significance.  This has nothing to do with statistical significance which is a comparison of effects to MSE.  Do the factors/interactions have a practical significance?  Another way to say this is you should evaluate the model in terms of scientific or engineering merit.  Are there rational and logical hypotheses that support the identification of interesting and not interesting terms?

2. R-square-R-square adjusted delta.  As you remove uninteresting term from model, the delta should diminish.  Also the size of the R-square adjusted.

3. Residuals.  How do they look?  Are there any outliers, unusual patterns, etc. as you remove terms?

4. p-values.  These might be useful for the first cut, but they are less useful (or useless) as you iterate.  What happens to the insignificant mean squares?  They are added to the MSE WITH the DF's essentially decreasing the MSE and increasing the F-values in a biased fashion.

5. Useful.  The model must be useful.  The mission is not to create the most complex model you can get, but to create a model the is predictive and useful.

Of course, one of the advantages of JMP is the ability to quickly change the model and re-evaluate.

[#5]

In answer to your question, "Otherwise, what is the purpose of performing it...". By 'it' I assume a designed experiment...I'll answer that from my admittedly somewhat biased frame of reference coming from industry as opposed to a research environment.

Far and away the primary purpose for conducting our designed experiments was not to '...make inferences...'. But to solve a practical problem. I'm not saying searching for 'inferences', which I'll define as new novel knowledge, isn't a worthy endeavor...it's just not how we found ourselves. So what is the ultimate purpose for conducting these designed experiments? If it's to solve a practical problem...then I'd try it both ways...modeling with and without the 'insignificant' terms and view the utility of the model in the context of solving the practical problem at hand. If it's new knowledge, then I'd consider additional experimentation before making blanket statements like 'no/minimal effect' to expand the inference space under different noises (suppliers, equipment, operators, scalability, and on and on) and nuisance variables and other issues, like factor level spacing, measurement system noise, ...and rarely is this accomplished with one experiment. Where I worked, we called this, ' understanding representation risk'.

A simple purely illustrative example, but situation we encountered more often than any of us would have liked. We would run a DOE on pilot equipment and make an inference 'that coating speed' has no effect on the response of interest. But then we scale up to production equipment...and all of a sudden 'coating speed' does have an effect. How can this be? New process...new noises. It's about how 'representative' the experiment is to future conditions. Deming wrote at length about the issues associated with enumerative vs. analytic studies.

Enumerative vs. Analytic Studies 

Only by understanding this wide landscape can one confidently approach making blanket statements like, 'no/minimal effect'.

[#6]

Considering these responses, I would argue that the JMP DOE learning module oversimplifies the analysis of a DOE.

[#7]

To be fair, JMP learning modules are meant to introduce the product and to "sell the product".  I spend 6 months teaching the basics of experimental design with multiple hands-on experiments and many practical case studies.  IMHO, it would be nearly impossible to teach this on-line (although I tried during Covid).  The learning modules are meant introduce the methodologies and expose individuals, with perhaps no prior knowledge, to the potential applications.  At the end of those modules if you can identify situations that would benefit from the methodologies, they have served their purpose.

I have a slightly different view than Pete regarding the use of experimental design.  IMHO, there are two "motivations" that drive investigative work:

1. Explanatory- A problem exists and you are trying to understand the problem and what may be causing it.  Of course DOE may be useful here, but I am biased to using directed sampling and components of variation studies to understand these events.  I can certainly make a problem occur with DOE, but that may not be why the problem occurred in the first place.

2. Prediction- Understand causality to enable the investigator to develop a useful prediction model.  This is where DOE shines and really there is no other methodology as powerful as DOE.

[#8]

Thank you for explaining.

View more...

Removing non-significant terms can simplify a model, but it’s important to consider the context, model assumptions, and potential multicollinearity. A non-significant term doesn’t necessarily mean that the factor has no effect; it may indicate insufficient power or improper measurement. Model reduction also applies to REML/mixed models, but caution is necessary. During my college years, I often sought help with writing my academic essays. After conducting some research, I came across DoMyPaper, which had many positive reviews. I decided to visit domypaper.com for help and it turned out to be a great experience. DoMyPaper has a team of experts who assist students in improving their writing skills. Now, I rely on their services to get help with my academic writing work.

[#9]

Hi @SaraA,

The examples shown in JMP modules are here to bring the design & analysis basics to non-statisticians who would like to "get started". Obviously the datasets are easy to follow up, and analysis is simplified, so that everyone can understand and try it. 

But as @statman mentioned, the topic of modeling is a lot more vast (and sometimes complicated) than "only" relying on p-values. Depending on your objective(s), you may have different paths to models evaluation and selection :

• Explainative model : In an explainative mode, you're more focussed on the terms that do have some influence on the response(s), so you might evaluate the need to include the different terms based on statistical significance (with the help of p-values and a predefined threshold for it like 0.05) and practical significance (size of the estimates, selection based on domain expertise). R², R² adjusted (and the difference between the two, which needs to be minimized) might be good metrics to understand how much variation is explained by the identified terms, and select relevant model(s) to explain your system under study.
• Predictive model : In a predictive mode, you're more focussed on the terms that help you minimize prediction errors, so you might evaluate the need to include the different terms based on how this improve the predictive performances, through the visualizations of actual vs. predictive plot, and size of the errors (residuals plot). RMSE might be a good metric to assess which model(s) have the best predictive performances (goal is to minimize RMSE).

You might also be interested by a combination of the two parts, so different metrics could be used to help you evaluate and select model's, like information criteria (AICc, BIC) that help find a compromise between predictive performances of the model and its complexity. To evaluate and select a model based on these criteria, the lower the better. You might also use maximum likelihood which is similar but does not include a penalty for the complexity of the model.

I would recommend to be cautious about p-values and avoid the "Cult of Statistical Significance" : Solved: Re: Statistical Significance - JMP User Community

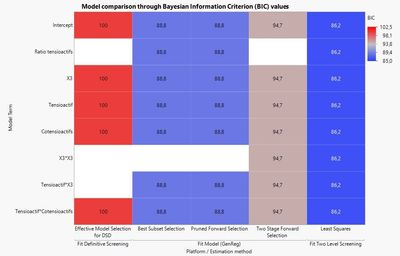
To create your model, there are a lot of platforms available in JMP (Fit Model and Generalized Regression models, Fit Two Level Screening, Fit Definitive Screening, ...), that use different techniques, estimations or validation criteria, sometimes depending on your design choice. You can try them and see how and when your model agree and when/where they disagree. Try plotting the outcomes of your different results through Raster plots or easier plots like this one :  

Depending on the platform used, you can check how well the models are in agreement, and with the use of a specific metric adapted to your objective, you can more easily choose on or several models.

Coming back to your original question, statistical significance and practical significance should be considered when modeling  response(s), and the resulting model should be confronted to domain experts as well as experimental validation.

Hope this complementary answer might be helpful, even if late,