- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Discussions
Solve problems, and share tips and tricks with other JMP users.- JMP User Community
- :
- Discussions
- :
- Re: Model comparisons
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Model comparisons
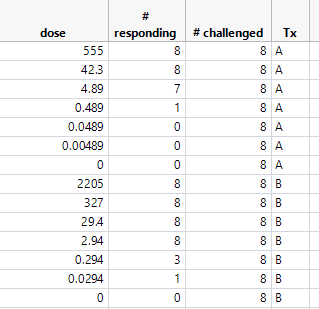
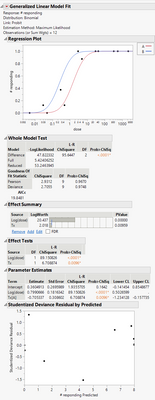
I have dose response data for two different treatment groups (see table below), and want to compare the dose response curves. I have run the analysis in the screenshot below, and the effects test shows that both dose and the treatment (Tx) are significant factors. What statistical test is JMP using to do the comparison shown under Effects Tests? Any help would be greatly appreciated.
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Model comparisons
It is not a t-test.
The column header in the Effect Tests is "L-R ChiSquare." This header indicates that it is a 'likelihood ratio test." The test statistic is twice the change in the likelihood function when the term is added to the model. This statistic has a chi square distribution. It is analogous to using a t-test of the estimate versus zero or a F-test of the sum of squares, which cannot be used in this case because the response is not continuous. It is categorical (counts), so it must be based on probability.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Model comparisons
Hi @tox ,
You can read more about Effects Tests here. I think in your case it's basically performing a t-test on the estimate for that factor and comparing that value to the null hypothesis, which would be the estimate for the factor is 0. So for your case, the p-values are small and you can reject the null hypothesis and conclude there is enough evidence to accept the alternative hypothesis, which is the factors and their estimates are significant in the model.
Hope this helps,
DS
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Model comparisons
It is not a t-test.
The column header in the Effect Tests is "L-R ChiSquare." This header indicates that it is a 'likelihood ratio test." The test statistic is twice the change in the likelihood function when the term is added to the model. This statistic has a chi square distribution. It is analogous to using a t-test of the estimate versus zero or a F-test of the sum of squares, which cannot be used in this case because the response is not continuous. It is categorical (counts), so it must be based on probability.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Model comparisons
Thanks for the answer on this. One other quick question - is there a way to have JMP display the prediction expression for the curves? I know this is a menu option under other models, but I don't see it here. Thanks again!
Recommended Articles
- © 2026 JMP Statistical Discovery LLC. All Rights Reserved.
- Terms of Use
- Privacy Statement
- Contact Us