Mixed Model Platform

[#1]

Hello, I have a rather large data set where I am trying to assess how mercury in finish caught in New Hampshire has varied from 1992-2021 and assess how these mercury levels vary from county to county throughout this time line.

My data is as follows

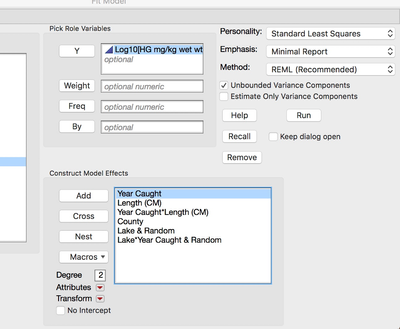
DV = Total Mercury (Log10 scaled, Continuous)

IV Fixed 1= Fish Length (Continuous)

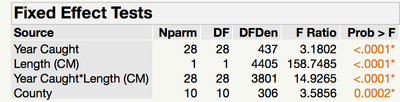
IV Fixed 2= Year Caught (Categorical, Numeric/Nominal)

IV Fixed 3= Year Caught * Length

IV Fixed 4= County (Categorical, Character/Nominal)

IV Random 1= Lake (Categorical, Character/Nominal)

IV Random 2= Lake * Year Caught

I have specified this in the Fit Model Platform Here.

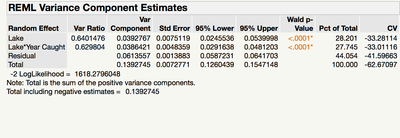
These are my output results

I am curious as to 

1. How should I interpret the Coefficient of Variation values in the REML output menu? (these values are also coming up as negative)

2. How to meaningfully Interpret the negative intercept as my parameter estimate as it is impossible to have a negative baseline mercury concentration

3. How to interpret both inter and intra group variation of the random effects (variation in fish mercury within lakes, between lakes, and across lake-year) 

4. How to back-transform my LS Means from the effect details red triangle drop down menu. 

I am also interested in seeing if there is something else I would need to do/explore given that this is my output? 

Thank you for your insight into this.

[#2]

Hi @IWRRI  : A few things:

1. The CV is 100*sqrt(VC)/mean, where the VC is the respective Var Comp. It is negative because your mean is negative (I'll get to that in 2 below).  But, these CV's are for the log-scaled data.  You are interested in the raw scale. In that case, CV = 100*sqrt(exp(Var Comp)-1) in Excel-speak. For example, for the Lake random effect, your Var Comp = 0.0392767. The CV (in untransformed scale) is then 20.01455169.  More about CV here.https://en.wikipedia.org/wiki/Coefficient_of_variation#Log-normal_data

2. The intercept is negative in log scale (not the raw scale).

3. This is an involved question. The very short answer is this is a partitioning of total variability...so you can see where variability comes from and perhaps prioritize your resources. 

4. You can do this "manually" via saving the output and back-transforming  the LSMeans (e.g., 10^LSMean) and their respective intervals. Careful with interpretations though; differences in arithmetic means in log-scale transform back to ratio of geometric means in the raw scale.      

[#3]

Hi @IWRRI,

Just some remarks on a general point of view :

• I'm not sure to understand why/how the variable lake can be a random variable and not County (which sounds also to be a location variable, and "as random" as lake since it is observational data ? So only a fraction of all possible locations, aka a random sample from a bigger population) ?
• Same question for Year, I don't see why/how it is considered as a fixed effect, since it is an observationaly study, you can't control time, and you may be more interested in the variation/variance per year than in the mean value per year ? And the years in the analysis (1992-2021) are just a random sample from bigger timeframe possible. 
• I would also recommend using the "Mixed Model" platform instead of "Least Squares" method since you have a combination of random and fixed effects : Mixed Models and Random Effect Models (jmp.com)

Since I don't know exactly your topic, some of my questions may sound naive or not appropriate for your topic. If so, you can ignore them. I hope these questions and remarks may help you,