- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Discussions
Solve problems, and share tips and tricks with other JMP users.- JMP User Community
- :
- Discussions
- :
- Re: Manual Calculation of the Shapiro-Wilk Test Statistic
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Manual Calculation of the Shapiro-Wilk Test Statistic
Hello Everyone,
Does anyone know how to implement manual calculation of the Shapiro-Wilk test statistic in JMP?
Using JSL script and/ or column formulas?
I know that JMP natively does this calculation natively in Analyze>Distribution and then Continuous Fit>Normal>Goodness of Fit, but I'm trying to reproduce the calculated value of the test statistic in order to understand it's basis with greater depth.
There are a number of useful clues in references online, but I'm having some difficulty putting the pieces together:
https://en.wikipedia.org/wiki/Shapiro%E2%80%93Wilk_test#cite_note-8
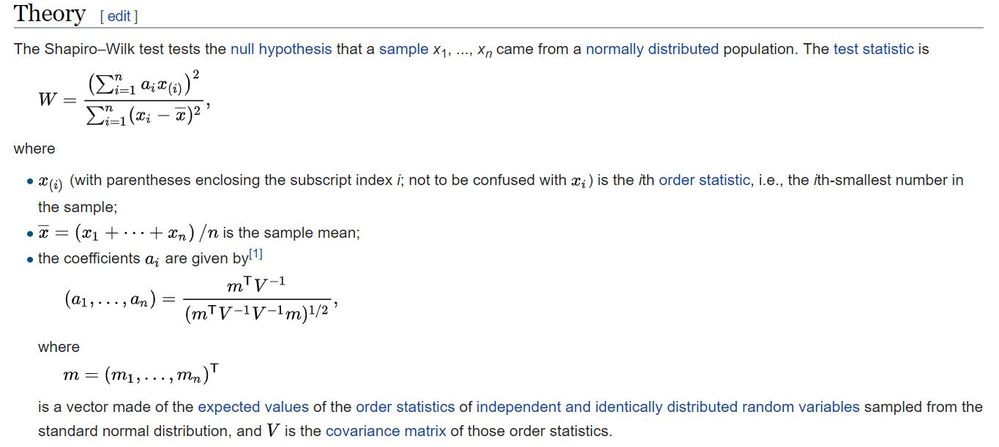
Here's the basis for it summarized nicely from Wikepedia link above:
Also some helpful clues here using MS Excel.
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Manual Calculation of the Shapiro-Wilk Test Statistic
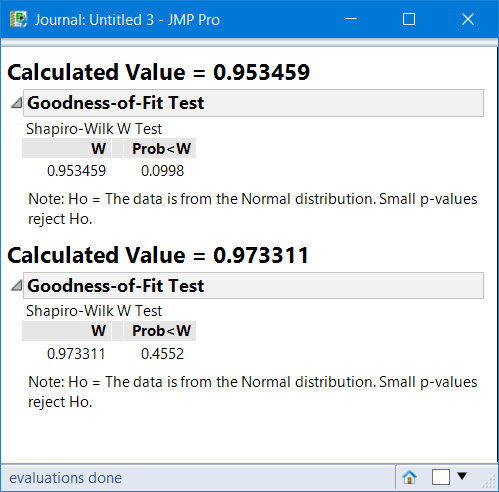
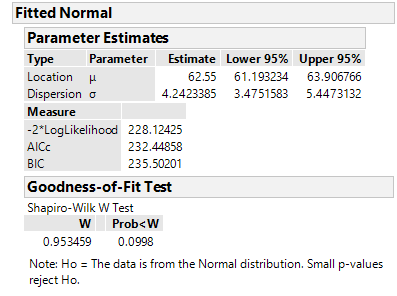
@PatrickGiuliano I am not sure why you would want to do this manually, when you have JMP that can produce the statistics and you can extract it from a report. A simulation where the sample size is the same so the weight coefficients are the same, meaning the weights are calculated once and used many times, might be a good scenario for doing this by hand/matrix.
That said, I found references for the coefficients and an algorithm to get them. The references are reported in the attached script. Here are the results of two tests with N=40.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Manual Calculation of the Shapiro-Wilk Test Statistic
Here is a link that does a step by step calculation that you might be able to use.
http://blog.excelmasterseries.com/2015/05/how-to-create-completely-automated_4.html
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Manual Calculation of the Shapiro-Wilk Test Statistic
Ignore this...I did not read your request very closely...sorry
JMP calculates the Shapiro-Wilk's test.
Open a data table.Go to Help > Statistics Index> find Shapiro-Wilk test for normality on the left, then press launchSelect which columns of your table to be tested
The test is available in JMP PRO 12 and higher.
It is the Goodnes of Fit test for a Normal Fit. The JSL is
Distribution(
Continuous Distribution(
Column( :height ),
Fit Distribution( Normal( Goodness of Fit( 1 ) ) )
)
);
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Manual Calculation of the Shapiro-Wilk Test Statistic
@PatrickGiuliano I am not sure why you would want to do this manually, when you have JMP that can produce the statistics and you can extract it from a report. A simulation where the sample size is the same so the weight coefficients are the same, meaning the weights are calculated once and used many times, might be a good scenario for doing this by hand/matrix.
That said, I found references for the coefficients and an algorithm to get them. The references are reported in the attached script. Here are the results of two tests with N=40.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Manual Calculation of the Shapiro-Wilk Test Statistic
Recommended Articles
- © 2026 JMP Statistical Discovery LLC. All Rights Reserved.
- Terms of Use
- Privacy Statement
- Contact Us