- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Discussions
Solve problems, and share tips and tricks with other JMP users.- JMP User Community
- :
- Discussions
- :
- MANOVA defining M-matrix, what am I testing
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
MANOVA defining M-matrix, what am I testing
Dear all,
In Fit Model after selecting MANOVA I need to specify the response type (or define the socalled M-matrix). Standard in other software (SPSS, JASP) the IDENTITY Response is used (identity m-matrix). I was wondering if there is a more elaborate explanation of what the other Response mean for the interpretation of your data and when they are useful for which hypothesis test. Say I have a construct of 5 items in a questionnaire capturing Information in some sort of way, what would it mean for the interpretation of this construct if I use different Response types.
Thanks in advance,
rene
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: MANOVA defining M-matrix, what am I testing
Hi @RvEDelft : The following link is probably the best place to start.
https://www.jmp.com/support/help/en/17.1/index.shtml#page/jmp/response-specification-panel.shtml#
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: MANOVA defining M-matrix, what am I testing
Dear Levei,
Thank you fro your interest and support. Before putting this request online I already read this information. I get the technique behind it. But it is the interpretation of the Response types I am looking for. I am used to define, interpret and using contrasts in SPSS. Deviation looks somewhat as the Mean Responsed Type in JMP Manova. However, I am not familiar with the interpretation of the Multivariate Response Types offered in JMP. When I am searching the internet I do not find an answer to that question. I hope I make myself clear, once again thanks for your response.
Rene
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: MANOVA defining M-matrix, what am I testing
Hi Rene,
The M matrix allows you to test hypotheses between the different response parameters, which are shown in the default MANOVA report in JMP.
To relate to the example you posed (i.e., items from a survey), I'm using below the sample data table "Online Consumer Data.jmp" to run a relatively simple MANOVA model. Here, our outcomes are 3 items representing responses on a survey about the perceived reputation of an online website, and we just want to test the effect of the "Female" variable. Feel free to run this JSL script to follow along:
dt = Open("$SAMPLE_DATA\Online Consumer Data.jmp");
dt << Fit Model(
Y( :Reput_1, :Reput_2, :Reput_3 ),
Effects( :Female ),
Personality( "Manova" ),
Run
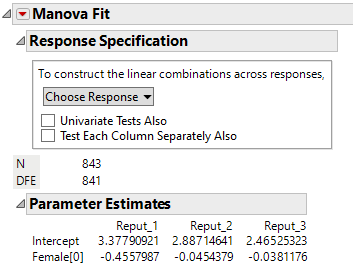
);The default report shows the matrix of Parameter Estimates of the model:
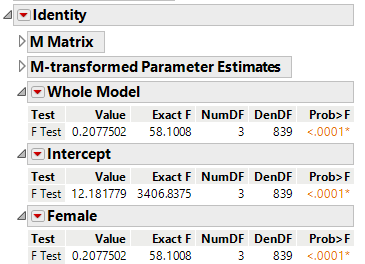
You can now use the "Choose Response" dropdown to start testing hypotheses between these response parameters. When M is the identity matrix, we're simply leaving the response columns of this Parameter Estimates' matrix unchanged and we're asking "is there an effect of Female overall in this multivariate system?" The answer is yes:
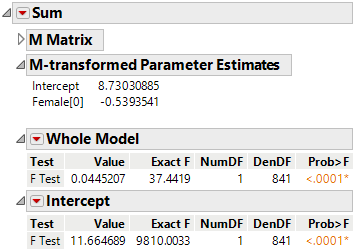
Notice that opening the "M-transformed Parameter Estimates" outline box will show you the unchanged Parameter Estimates (technically, the M matrix postmultiplies the Parm Est matrix, so that's how you get the transformed estimates). For additional interpretation, we'd say "yes, there's a significant difference between males and females in our responses" and looking over the estimates and/or the Least Squares Means plots can help interpret those results a bit more. But sometimes this isn't enough detail, such that someone might want to know if Female has an effect in a particular combination of the columns in the Parm Est matrix. Let's say we want to know if there's an effect in the sum across all our responses. For this, we select "Sum" under the "Choose Response" dropdown, and we can see the answer again is yes, there's a significant effect:
The interpretation here is much easier because Female has 2 levels and the "Sum" option resulted in reducing our Parm Est matrix into just a vector. So we can say "there's a significant difference between males and females when looking at the sum of perceived reputation on our 3 items. The negative Female[0] estimate indicates that males have a lower sum across these responses."
Using other choices of M for these data might not make any sense... for example, the "Profile" option is likely most useful for outcomes that represent repeated measures. If you hover over the "Profile" option, you'll find this description
which in our example, suggests that we're going to ask whether there's an effect of "Female" in the difference between item 1 and 2 and between item 2 and 3. I don't think this makes as much sense for these data, but if the data were repeated measures, this option would test time-to-time differences "are there differences across males and females from one occasion to the next?"
As you know, there are other options for M in the output... by looking at the matrix and the transformed Parm Est, you'll be able to see what hypothesis is being tested.
Lastly, I'll add that the DF of a test unveils the level of "detail" you're getting from the test. Using the "Sum" option, we were able to be very specific about our interpretation, and that's no surprise because the DF = 1. The "Identity" option gave us a 3 DF test, which means we know there are differences but those differences are "somewhere" in our responses.
HTH,
~Laura C-S
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: MANOVA defining M-matrix, what am I testing
Oh! I'll add that if you have survey data as you described, the Structural Equation Models platform might be particularly helpful, as it can model your construct directly and account for measurement error in your models.
Recommended Articles
- © 2026 JMP Statistical Discovery LLC. All Rights Reserved.
- Terms of Use
- Privacy Statement
- Contact Us