- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Discussions
Solve problems, and share tips and tricks with other JMP users.- JMP User Community
- :
- Discussions
- :
- Re: Linear Mixed Model
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Linear Mixed Model
Dear all,
I am a rooky in statistics and this is the first time I'm using jmp, but I have some knowlegde about spss. I first tried to do it by myself, but it's too hard. I hope some of you could help me with the following:
I have collected soil samples of 3 different locations (with totally different soil types and weather conditions) and measured the pH, EC and C/N. There are experimental site established on each location. Each location contains 2 plant varieties and each variety has 2 different treatments. One is Control, and the other is amended with extra fertilizer (nitrogen and phosphorus).
What I want to do is, is analyzing the the effect of the treatment. Therefore, I want to use LMM.
What I think is what is right: location and variety are random factors. However, I'm not sure whether I should include the variety in my model. And the fixed factor is 'Treatment'.
And, I don't know how I should check the normality of the error term. You just put those factors in 'Contruct model effect' without the interaction of the factors?
Kind regards.
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Linear Mixed Model
Hi @Ashya,
Welcome to the community!
I agree that the location is probably a good candidate for a random effect, but I would think plant varieties would be fixed along with treatment. It wouldn't necessarily be wrong to treat variety as random, but it seems a bit odd unless the varieties you tested were selected to be a representative sample of all varieties that you would like to generalize the results to. Having other fixed effects other than treatment does not diminish your ability to compare the efficacy of the treatment across plant varieties.
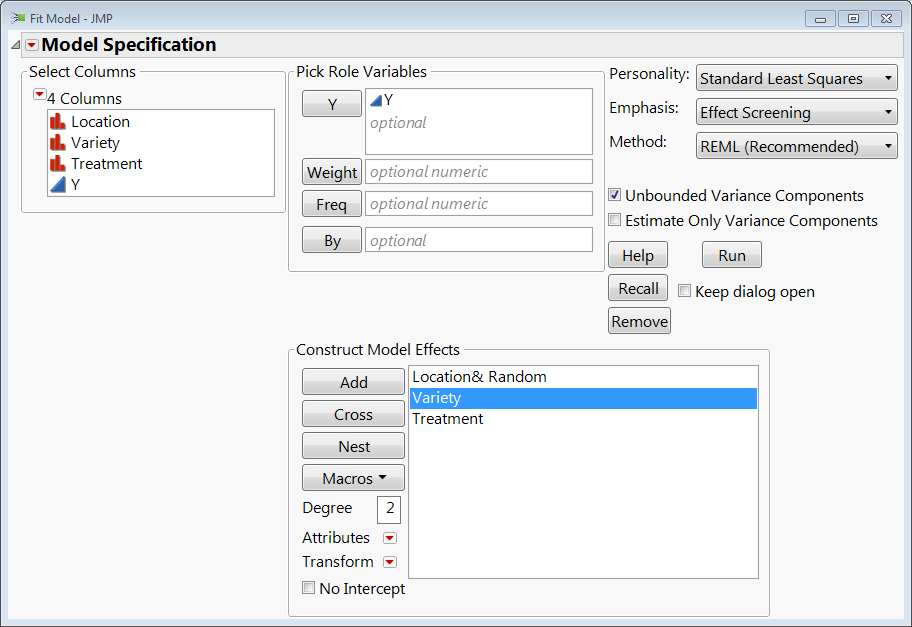
You can fit the appropriate model several ways in the Fit Model platform if you have JMP Pro. The Mixed Model personality in Fit Model is preferable if you have Pro. If you have just have base JMP, you can specify your model this way:
Again, you can treat variety as random if you really want to. I would definitely not exclude it, because if it does explain a lot of the variance, excluding that term will cause all the variance explained by variety to go into the residual noise, and your test for the treatment effect will by less powerful.
As far as checking assumptions, you'll want to do that based on conditional residuals rather than regular ("marginal") residuals because the marginal residuals don't consider random effects and may cause the diagnostic plots to look like they fail the assumption. To get the conditional residuals without JMP Pro, go to the red-arrow in the report window > Save > Save Conditional Residuals. Then you'll need to plot them in distribution to check normality with a normal quantile plot or Shapiro-Wilk test for goodness-of-fit after fitting a normal distribution to the conditional residuals.
You can similarly plot the conditional residuals on a run chart to check for independence. If you want to create a residual vs. predicted plot, you'll also want to save the conditional predicted values and then construct the plot in something like Graph Builder.
If you do have JMP Pro, you can get all the conditional residual plots within the Fit Model report with the Mixed Models personality, which is really nice.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Linear Mixed Model
Hi @Ashya,
Welcome to the community!
I agree that the location is probably a good candidate for a random effect, but I would think plant varieties would be fixed along with treatment. It wouldn't necessarily be wrong to treat variety as random, but it seems a bit odd unless the varieties you tested were selected to be a representative sample of all varieties that you would like to generalize the results to. Having other fixed effects other than treatment does not diminish your ability to compare the efficacy of the treatment across plant varieties.
You can fit the appropriate model several ways in the Fit Model platform if you have JMP Pro. The Mixed Model personality in Fit Model is preferable if you have Pro. If you have just have base JMP, you can specify your model this way:
Again, you can treat variety as random if you really want to. I would definitely not exclude it, because if it does explain a lot of the variance, excluding that term will cause all the variance explained by variety to go into the residual noise, and your test for the treatment effect will by less powerful.
As far as checking assumptions, you'll want to do that based on conditional residuals rather than regular ("marginal") residuals because the marginal residuals don't consider random effects and may cause the diagnostic plots to look like they fail the assumption. To get the conditional residuals without JMP Pro, go to the red-arrow in the report window > Save > Save Conditional Residuals. Then you'll need to plot them in distribution to check normality with a normal quantile plot or Shapiro-Wilk test for goodness-of-fit after fitting a normal distribution to the conditional residuals.
You can similarly plot the conditional residuals on a run chart to check for independence. If you want to create a residual vs. predicted plot, you'll also want to save the conditional predicted values and then construct the plot in something like Graph Builder.
If you do have JMP Pro, you can get all the conditional residual plots within the Fit Model report with the Mixed Models personality, which is really nice.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Linear Mixed Model
Hi!
Thank you very much for your answer!
I tried what you said, but the conditional residuals did not have a normal distribution. I tried to transform with log(y), but it didn't work. Do you maybe have another suggestion for this? And also, to get the conditional residuals, it was not needed apply 'full factorial', right?
Kind regards
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Linear Mixed Model
How big is your total data set? Post the normal quantile plot and I can assist you from there.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Linear Mixed Model
there are 215 samples.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Linear Mixed Model
Your tails are a little heavy, but it's really not that severe. Depending on your comfort level, you could justify not taking any corrective action. Your model is probably not biased in any way by the heavier tails, but your prediction intervals could be a little narrower than they should be.
If you want to address it, I recommend just treating everything as fixed effects temporarily so you can dig a little deeper. Do a full factorial model with all your model terms and look at the residuals to see if they are more normal. If they look good, see if any of the additional model terms are significant. If they are, you can incorporate them into your mixed model and re-run.
You can also try a Box-Cox analysis in Fit Model while you're treating all the effects as fixed (not available for mixed models) as long as the data points are all positive. Since your response is pH, I'm guessing that will not be a problem. This will recommend a power transform that will best "normalize" the residuals.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Linear Mixed Model
Thank you!
I tried your first suggestion, but the residuals were still not normally distributed.
And about your second suggestion, I did the test, but I don't really understand what to do with this. Could you enlighten me?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Linear Mixed Model
Sure. So Box-Cox recommends some optimal transformation to make your variance more homogenous and the residuals more normal. Basically, it evaluates the SSE for the model across a range of power transforms (y^λ), except the value λ = 0 indicates a natural log transform. The transform that minimizes the SSE is the "best" transform. However, bottom of the curve is usually kinda flat, so you can choose various transformations within a neighborhood. You usually want to pick one that corresponds to something meaningful. For example, if Best λ = -0.98, I would choose to take the inverse because -0.98 is really close to -1.
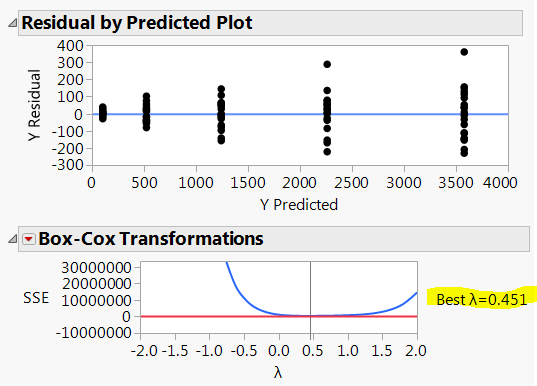
Here's an example: I generated a linear model using normal errors and squared all the response values. I should expect Box-Cox to tell me I need to take the square root to have normal data again. Here's what I actually got:
You can see that the "best" transform is 0.451, but I know the real answer is 0.5 and this is really close. If I didn't know the real answer, I would still choose 0.5. You can re-run your model with your desired transform by clicking the red-arrow next to "Box-Cox Transformations" and selecting "Replace with Transform." You'll get a pop-up box that asks you to type in the value you want. Press OK and you'll get a new Fit Model with the transformed response.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Linear Mixed Model
So, after the Box cox is applies, the distribution of the risuals should be normal, right? In my case, it isn't...
Is there maybe another statistical test I can use to analyse my data?
Recommended Articles
- © 2026 JMP Statistical Discovery LLC. All Rights Reserved.
- Terms of Use
- Privacy Statement
- Contact Us