- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Discussions
Solve problems, and share tips and tricks with other JMP users.- JMP User Community
- :
- Discussions
- :
- Lack of fit test
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Lack of fit test
Hi all JMPers,
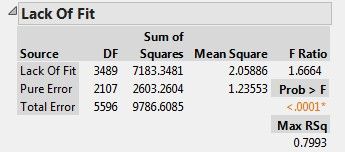
Does anyone know what saturated model is used in the LACK OF FIT test? More specifically, when running Fit Model, say by Standard Least Squares, I get the table of Lack Of Fit as following:
My understanding is that:
1) p-value gives me that the model can be improved by adding interaction terms,
2) Max RSq is obtained by the saturated model.
Is my understanding correct? If so, is there a way I can get the saturated model in JMP?
Thank you all!
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Lack of fit test
Yes, your understating is correct.
If so, is there a way I can get the saturated model in JMP?
Yes, you can run such model with some data prep.
(Caution-a saturated model is over-parameterized to the point that it is essentially interpolating the data. It is not a sound modeling practice.)
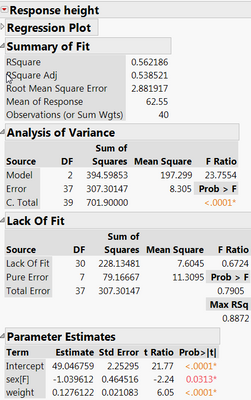
(1) The screenshot shows a linear regression fit to predict HEIGHT with SEX and WEIGHT as predictors. Although this main effect model doesn't appears to be under-fit, Max R Sq indicates a saturated model would achieve R Sq at 0.8872.
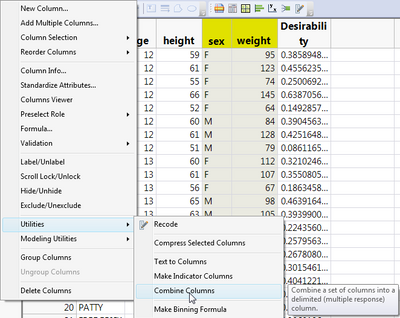
(2) To do this Combine predictor variables to form a grouping variable, SEX_WEIGHT, so that I can assigns a parameter to each unique combination of the predictors. Use the Combine Columns to get it
(3) Refit the model using SEX_WEIGHT as the predictor . As shown, R Square is indeed 0.8872. There are 32 parameter estimates (plus intercept) in the model.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Lack of fit test
Yes, your understating is correct.
If so, is there a way I can get the saturated model in JMP?
Yes, you can run such model with some data prep.
(Caution-a saturated model is over-parameterized to the point that it is essentially interpolating the data. It is not a sound modeling practice.)
(1) The screenshot shows a linear regression fit to predict HEIGHT with SEX and WEIGHT as predictors. Although this main effect model doesn't appears to be under-fit, Max R Sq indicates a saturated model would achieve R Sq at 0.8872.
(2) To do this Combine predictor variables to form a grouping variable, SEX_WEIGHT, so that I can assigns a parameter to each unique combination of the predictors. Use the Combine Columns to get it
(3) Refit the model using SEX_WEIGHT as the predictor . As shown, R Square is indeed 0.8872. There are 32 parameter estimates (plus intercept) in the model.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Lack of fit test
Thanks a million!
This is a great answer, although I didn't find the Combine Column, I am using JMP Pro 11.0, but I got the idea.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Lack of fit test
Yes, Combine Columns along with many other column utilities were added in JMP 12.
Recommended Articles
- © 2026 JMP Statistical Discovery LLC. All Rights Reserved.
- Terms of Use
- Privacy Statement
- Contact Us