Lack of fit in face-centred composite design

[#1]

Greetings.

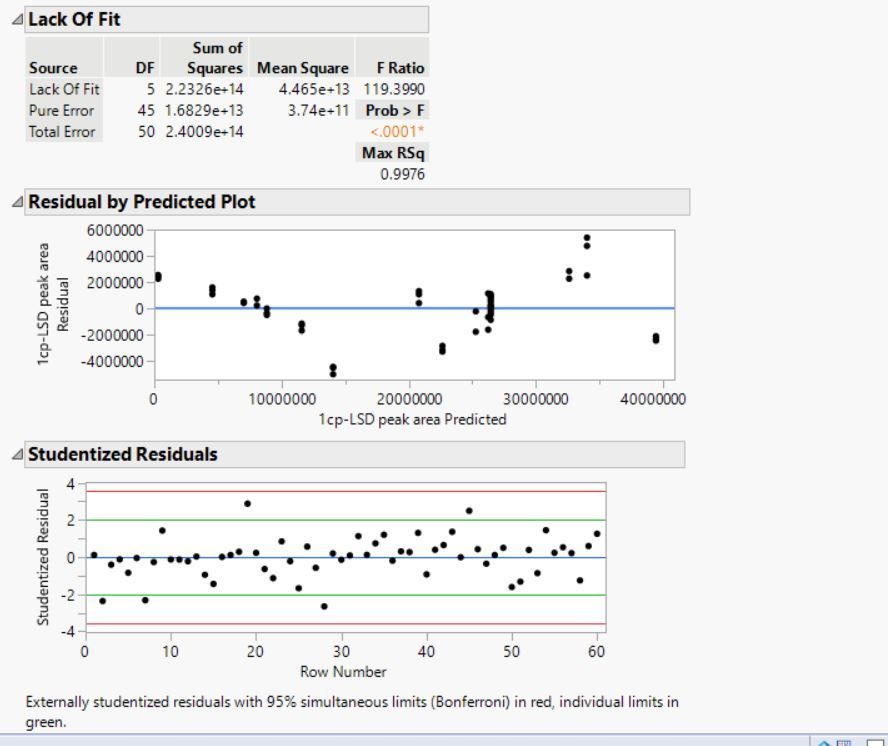
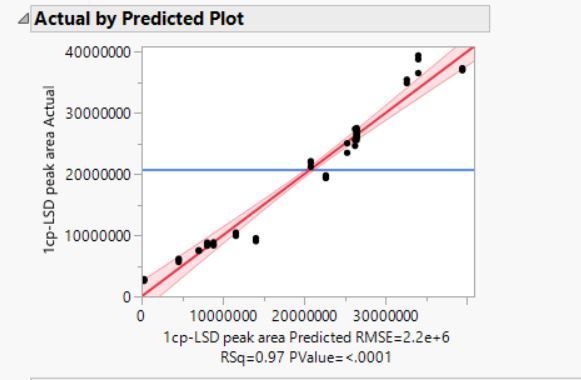
I am a PhD student from non-engineering background and has been using JMP 17 Pro for the past one month. This is my first-time using JMP software and I made self-study through JMP website, YouTube, and Chemistry World to be able to arrive to RSM but I am struggling to troubleshoot the lack-of-fit issue. I started off my optimisation process with fractional factorial design (2^6-2) to screen the important factors using 2-level screening. From there, I made a face-centred composite design for three significant factors using a slightly wider trajectory with six additional centre points, in triplicates with random order of run using RSM in classical design. The output was 60 experiments including 18 centre points for multiple compounds measuring signals. I only had two compounds with insignificant lack-of-fit, the rest of them P<0.001. My question is:

1. How can I check if the high number of centre points causing the biasness in the modelling for other compounds?

2. Is it okay to remove the centre points and keep all other response for modelling?

3.How to check the if the model in the JMP fits the quadratic or any higher order polynomial to adjust it before tweak the instrument. 

4. I read @Phil_Kay suggested the use of Best Subset and SVEM Lasso in Gen Reg for similar issue in another post. Where can I find more detail about data analysis using those two approaches to fit the RSM to get desired lack-of-fit in DOE? 

5. If that is not the case, how to augment the experiment to achieve desired the lack-of-fit? 

Please assists me.

Thank you

Residuals PlotActual versus Predicted Plot

[#2 · Accepted solution]

Hi @dNADA,

Welcome in the Community !

Have you checked first the explanations given in the JMP Help about Lack-of-fit test ? : Lack of Fit (jmp.com)

Here are my responses to your questions, based on limited information available :

1. I'm not entirely sure to follow the different designs steps : you have first created a fractional factorial design, and from this design, augment it to a CCD for the three detected significant factors, is that correct (or created a new CCD without augmenting) ?
   I don't understand how centre points can "cause bias" in the modelling ? Since your centre points are replicates, have you checked the variability of the response measured on these points ? Is the variability low enough compared to your domain expertise and any repeatability/reproducibility study ?
   If you have done a design augmentation, during the augmentation, have you grouped new runs into separate block to account for measurement change between the two steps ?
   The Lack-of-fit test is an indication that the model you specified may have too many terms, or not enough compared to the data you have : it compares the pure error estimated from your replicate runs (centre points) to the rest of the error (total error - pure error).  
   
   
2. No, you shouldn't remove any points if you have not justified you "can" do it, based on statistical properties (outliers, ...) AND domain expertise (erroneous values, typo in the measurement recording, bug/problem in the measurement system, ...).
   In your example, you can still compare the outcomes of two models, one normal with all points, and the other one by "hiding and excluding" the centre points runs, and see if the outcomes are very different or not. But you may check before some other options, like measurement variability of your responses compared to variability in your model (RMSE), significance of terms in the model, ...
   
   
3. It may be difficult to help you with only the two screenshots you provided, as I'm not entirely sure how you build your DoE and how you did the modeling. But you can see which terms are entered in the model in the "Effect summary", "Parameter Estimates" or "Effect Tests" panels (available in the red triangle next to each response, and then in "Regression Reports" or directly in the red triangle menu for "Effect Summary"). If you have done an RSM design like CCD, you should be able to create a model with all main effects, 2-factors interactions and quadratic effects.
   Do you already have these type of terms in your model ? Which ones are significant ? It would help having the JMP table to see if the model could be refined before thinking about higher order terms or something different.
   From your residual plots (and actual vs. predicted), it seems there is some curvature that may not be properly handled by your current model, so you may check if you have interactions and quadratic effects in the model. If you already have them, maybe higher order terms may be required. 
   You will not be able to take properly into account higher than quadratic effects in your model if you have a CCD design, since you have 3 levels per factors (min, medium and max), so you can only fit quadratic effects max. You would need 4 levels by factors to fit 3rd order terms, 5 levels to fit 4th order terms, etc... so it would require a design augmentation if you need these terms in the modeling.
   
   
4. You can have more infos on different estimation methods from GenReg here : Estimation Method Options (jmp.com)
   
   
5. If you can't create a "good" model based on your design and data (and perhaps you need indeed some higher order terms), from your DoE table you can click on "DoE", "Augment Design" and specify your factors and responses : Augment Designs (jmp.com) 
   From there, you can "Augment" your design (and group new runs into a new block) and specify which other terms you would like to have in your model in the "Model" panel. 

I hope this first answer will be informative for you,

[#3]

Hi,

All the advice from @Victor_G  is sound. I also think it is hard to give a full answer without understanding more about what you have done. Screenshots are good but attaching some illustrative data as a .jmp table is much more helpful.

I think I know what you mean by asking if the centre points are biasing the lack-of-fit statistic. The 18 CPs will have a strong influence on the calculation of pure error, which is used in the lack of fit test. If the error variance at the centre of the design is not representative of the error variance across the design as a whole (you might be able to think of reasons why this would be the case) then the centre points will be biasing the lack of fit test, at least to some degree. This is one of the reasons why some people prefer not to use centre points. However, it is also entirely possible that the centre point repeats are representative of the error across the whole factor space.

Are the triplicates really independent runs? That is, did you completely reset factors between the first and second of each triplicate, and between the second and third of each triplicate? Or is each triplicate just 3 repeated measures from the same preparation sample? If they are not truly independent runs, that would also affect the validity of the model and the lack of fit test, unless you add a random effect term for "preparation".

You should also consider that your lack of fit test could be completely valid and what that means. The lack of fit does not tell you whether your model is wrong or right ("all models are wrong"). Please don't just use lack of fit significance as a tick box exercise. Consider what it really means. Consider the size of the error terms and question whether that fits with your experience of the system. If lack of fit is "significant", is it actually important - it might not be.

If you think that the lack of fit is valid and important then you might want to look to add higher order terms to your model. I can't see your design, so I don't know what models will be possible to estimate. But you might want to test cubic (X1*X1*X1) and/or partial cubic (X1*X1*X2) terms in your model.

I hope this helps.

Phil   

[#4]

Both Victor and Phil have provided excellent advice and some great questions.  Try this, create a subset of the data table for just the center points.  Sort them in run order.  Plot them, you might use a X, MR chart or graph builder.  Are there any patterns or unusual data points?  Is the variation seen in the center points representative of "typical" variation in the process?  You likely need some SME help to analyze the data.

[#5]

In addition to the other great comments form @Victor_G  , @statman  , and @Phil_Kay  , the stud residual plot looks, perhaps, like there is some blacking going on that is unaccounted for; for the first 30 or so runs the residuals are skewed low, the next 20 or so are skewed high. Were all runs done all in one day? Across several days? Different analysts etc?

[#6]

Both pictures show plots that exhibit patterns from lack of fit. Notice how close replicates are compared to the deviations from the identity line in the Actual by Predicted plot or the deviations from Y = 0 in the residual plot? How was replication performed? Were the runs fully randomized? (Each run was selected in random order, and all the factors were reset before the next run?)