JMP > JSL > Best method to calculated signed Area Under the Curve for simple time series

[#1]

Hi JMP Community,

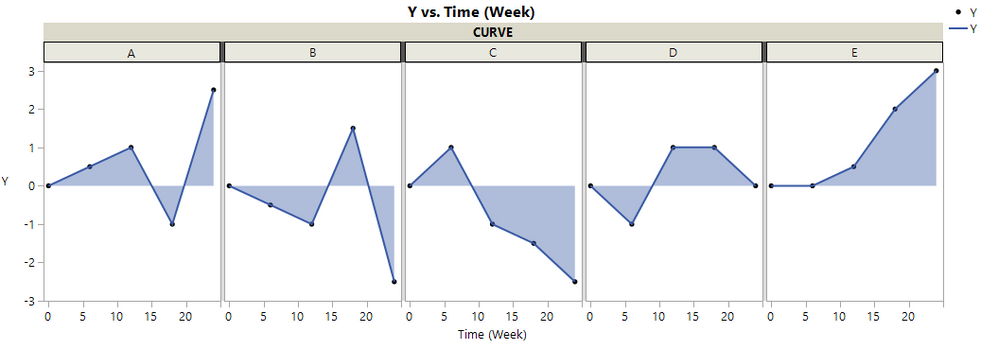
I need to calculate the signed area under the curve for simple time series data (see mock data below).

Specifically, I need to calculate the area (as shown in the graphs above) above zero as positive and below zero as negative, including local shift from positive to negative and reciprocally.

Examples:

• AUC for curve A = Positive Area 1 + Negative Area 2 + Positive Area 3
• AUC for curve C = Positive Area 1 + Negative Area 2
• AUC for curve E = Positive Area 1

The Polygon Area () function does not appear to handle the more complex time series correctly probably due to the crossing segments. Also, this function does not return the signed value for the area. Would you know of an Add-In or a function that I could use to achieve my goal?

Thank you.

Best,

TS

[#2 · Accepted solution]

Trapezoid Rule?  

Names default to here(1);
dt = current data table();
x_col = Column(dt, "Time (Week)");
y_col = Column(dt, "Y");
by_col = Column(dt, "Curve");


auc = function({x_col, y_col, by_col}, 
	{DEFAULT LOCAL}, 
	Summarize(dt, by_values=By(by_col));
	areas = [=>];
	for(i=1, i<=nitems(by_values), i++, 
		by_value = by_values[i];
		rows = dt << Get Rows Where(by_col[]==by_value); // get he rows for the curve
		x_values = x_col[rows];
		r = rank(x_values); // make sure it's ordered right
		
		x_values = x_values[r];
		y_values = y_col[rows][r];
		n = nitems(x_values);
		//trapezoid rule
		x_1 = x_values[1::n-1];
		x_2 = x_values[2::n];
		y_1 = y_values[1::n-1];
		y_2 = y_values[2::n];
		
		x_intervals = abs(x_2 - x_1);
		y_avg = (y_2 + y_1)/2;
		area = sum(x_intervals  y_avg);
		areas[by_value] = area
	);
	return(areas);
);
areas = auc(x_col, y_col, by_col);
show(areas); // areas = ["A" => 10.5, "B" => -7.5, "C" => -16.5, "D" => 6, "E" => 24];

Also, What you're doing isn't a polygon (in case you're using this elsewhere for similar things).  The area of a polygon can never be negative or it wouldn't exist. 
The example in the scripting index shows you what it's doing.  

Names Default To Here( 1 );
area = Polygon Area( {0, 0}, {0, 10}, {10, 10}, {10, 0} );

It closes the loop (in this case a square) between {10, 0} and {0, 0}.  So the polygon area is 100.  It doesn't matter where you put that in the x/y plane.  The area of a 10x10 square should be 100.  

Names Default To Here( 1 );
area = Polygon Area( {-100, -100}, {-100, -90}, {-90, -90}, {-90, -100} );
show(area); //100