- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Discussions
Solve problems, and share tips and tricks with other JMP users.- JMP User Community
- :
- Discussions
- :
- JMP Custom DOE vs Full Factorial DOE
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
JMP Custom DOE vs Full Factorial DOE
Hi,
I'm new to JMP. I would like to learn and understand the difference between the Custom DOE design and the Full Factorial DOE design. I am designing an experiment using 4 variables (2 levels each, 4th variable is categorical). A full factorial requires 16 runs. When I build the experiment in Custom design however, the default # of runs in JMP is 12. Why are the # of runs in each of these different? I get why it is 16 in the full factorial (2^4). But why is JMP recommending just 12 in the custom design? What's been assumed/factored into each of these designs?
I would greatly appreciate any help on this!
Thanks,
Sajith
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: JMP Custom DOE vs Full Factorial DOE
That's a whole course of study contained in that question, but I'll try to summarize as best I can. Custom Design is built on a completely different paradigm of "optimal" or "algorithmic" designs. Full factorial designs are a classical type of DOE. They enforce all possible combinations of factor levels into the design. This gives the design some very desirable properties, such as orthogonal effects (no correlation between model terms, so coefficients are estimated with maximal precision for given number of runs). You can also estimate all main effects and higher order terms up to n-way interactions for n factors. However, you'll find that these designs quickly explode in size. A full factorial with 8 factors, each with 2 levels, has 2^8 = 256 runs. In most cases that is way too many runs.
In classical designs, you would look to fractional factorials to reduce the number of runs. These designs strategically confound the higher order model terms in order to reduce the design size significantly. In many cases, experimenters are only interested in main effects and 2 factor interactions. So losing the ability to estimate an 8, 7, 6, 5, 4-way interactions is of little consequence. For example, I could do a fractional factorial with 8 factors in only 64 runs (quite a bit lower than 254!), and still have uncorrelated main effects and 2-factor interactions, and can maybe even estimate higher orders than that depending on the level of fractionization. These designs, amongst many other classical designs, are all derived from theory.
Optimal designs are generated from computer algorithms where you basically describe what you want as inputs into the algorithm, and it returns a design with the most optimal set of design points to meet your experimental objectives. It does so through a process of rearranging design points (aka your run conditions) inside the design space until some optimization criteria is optimized (maximized for some criteria or minimized for others). There are 2 really prominent optimality criteria, D- and I-optimality. D-optimality emphasizes precise estimates of model coefficients (makes it a pretty good all-around choice, but excels in screening situations where people would commonly choose fractional factorial designs). I-optimality emphasizes low prediction variance, and is more associated with response surface designs. The basic idea is that while classical designs are very rigid and uncompromising, optimal designs can tailor an experiment to your needs. I can do a decent design for the 8-factor situation with something like 48 runs and still be able to estimate all the model terms I care about (main effects and 2-factor interactions). I pay for this convenience by allowing some partial correlations between the model terms, but that is often of little consequence.
You will find other optimality criteria in Custom Design. A-optimality is a newer addition, and I think they are very compelling designs.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: JMP Custom DOE vs Full Factorial DOE
Thank you so much! That explanation was very helpful.
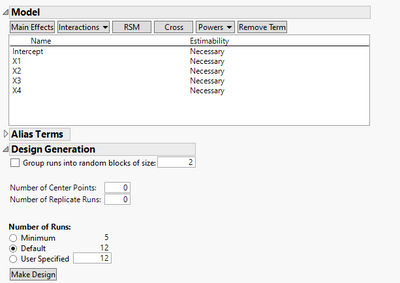
I'm guessing under Custom Design I would need to specify what higher order interactions I would like my model to estimate. For example, below is a screen shot of my design. Based on this, my design would only be able to estimate the main effects, is that correct? If I need higher-order interactions, I'm guessing I would need to specify under Model?
Thank you so much again for your help, Cameron!
Sajith
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: JMP Custom DOE vs Full Factorial DOE
Correct and Cameron's explanation is quite good.
I will say there are differing opinions on the use of Optimal designs...Optimal designs can provide a benefit fewer runs/resources, but not without risk.
The advantage of the classic fractional factorial is the ability to easily understand the aliasing, there is no partial aliasing. You can choose what you want to estimate and what you want to confound. This is very useful when you are going to iterate. The potential problem with Optimal designs, is the partial aliasing... it can be challenging to explain results that don't make engineering or scientific sense. It can be difficult to plan and execute the next experiment to de-alias confounded effects. Admittedly, I am extremely biased by my experience. I have found that experimentation is best done sequentially (what is the likelihood you have THE right factors tested at optimum levels in the first experiment?). The purpose of the first experiment is to design a better experiment. So the entire number of "runs" needed has little to do with the first experiment, but the entire study. While Optimal designs can save resources, they may sacrifice the advantage of the additivity of multiple fractional designs run iteratively. The other consideration regarding design selection is what you will do with noise...but that is another discussion.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: JMP Custom DOE vs Full Factorial DOE
I have a different opinion, but before I present it, I just want to say that the strategy and the principles of the design of experiments are invariant to the choice of the method of design.
A disadvantage of classical (regular) fractional factorial designs is confounding. (I expect that you don't like Plackett-Burman designs either, because they also lead to correlated rather than confounded effects.) Confounding might be easy to understand (I don't believe so) but I am still unable to estimate a lot of effects. The key screening principles guide my decisions about confounded effects but the principles are not guaranteed and so neither are my conclusions. The confounding pattern is arbitrary (minimum aberration design) for most users. I can choose the confounding to a limited extent but the task is not easy, and what would I change if I have little prior knowledge? So the classical designs have some risk, too.
Custom design asks me to specify up front what I want to estimate. It further allows me to identify primary and potential effects to produce a design that is optimal to a set of models when the model is uncertain. It then minimizes the correlation between estimates (D-optimal) so that estimation is possible for every effect, albeit with larger variance if the correlation cannot be eliminated. In the DOE strategy, I will do everything possible to maximize the effect size while minimizing the variance regardless of the design method. I can even manage the correlation more easily with an alias-optimal design.
The simplest of mixture experiments using a simplex design manage to succeed in spite of correlated estimates. It seems to me a good thing that there are no confounded effects with these designs.
Adding center points to a fractional factorial design introduces correlation of effects, too.
The augment design method in JMP (custom design with a fixed set of runs) is not difficult. It is the easiest and most flexible way I know to plan the next round of experimentation and grow the empirical evidence. I can specify new factor ranges, new model terms, and the number of new runs. There is no sacrifice.
Custom design will make the classical result when it is optimal for the given design specifications of the factors, models, randomization, and blocking. But custom design can make all the other designs in between the classical choices. Custom design offers many benefits besides economy. So why should I start with a classical design?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: JMP Custom DOE vs Full Factorial DOE
@SajithDnot to put too fine a comb to your second post showing the model specification window with only main effects, and a 12 run design...you can estimate select two factor interactions. Reason being you have sufficient degrees of freedom to do so. But as @statman points out...you'll want to insure you spend a few minutes with the Design Evaluation platform to understand the correlation among your parameter estimates. The 12 run design will be most efficient estimating ONLY main effects...but you can estimate two factor interactions.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: JMP Custom DOE vs Full Factorial DOE
To add two thoughts to @cwillden and @statman 's sound counsel:
1. Optimal design methods allow the experimental planning team to articulate specific combinations (the phrase is often called 'disallowed combinations') that you do NOT want included in the experimental design. Sometimes specific combinations are not of interest, or might cause a catastrophic failure of the system under study or safety hazard for equipment, people, or the environment. So JMP's Custom Design planning section allows for the experimenter to disallow these combinations. With Classical Designs, you get what you get based on the number of factors, chosen aliasing (if fractionating a design), and their levels.
2. Often times resources more than anything else dictate the number of runs in an experiment. Materials, equipment time, testing effort, all can play a constraining role. That's why JMP's Custom Design platform allows you to specify the exact number of runs you want to include in the experiment. Again, Classical Designs # of runs are 'you get what you get' without the ability to adapt the experiment to resource constraints.
Recommended Articles
- © 2026 JMP Statistical Discovery LLC. All Rights Reserved.
- Terms of Use
- Privacy Statement
- Contact Us