- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Discussions
Solve problems, and share tips and tricks with other JMP users.- JMP User Community
- :
- Discussions
- :
- Is there a correlation coefficient for multiple linear regression ?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Is there a correlation coefficient for multiple linear regression ?
Hello,
while I can display in simple linear regression a Pearson correlation coefficient to a specific R2/R2adjusted, can I, or is there a way to get a correlation coefficient for a multiple linear regression model, where two or more variables improve my R2adjusted significantly ? Many thanks, Marc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Is there a correlation coefficient for multiple linear regression ?
Hi Marc,
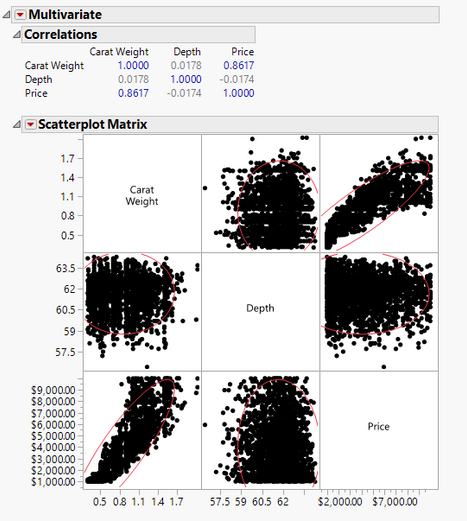
While we study on multiples input variables with output, we may get the correlations coefficients as per the menu path below:
Analyze > Multivariate Methods > Multivariate.
Hope this help to answer your question.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Is there a correlation coefficient for multiple linear regression ?
Marc,
I am not positive that @Elvic_OngGX answered what you were asking. My interpretation of your question, is that you want a single "r" value as in a Pearson correlation, that represents a Multiple Linear Regression. If my interpretation is correct, the answer is your R Square or adjusted R Square is that value. It represents the amount of relationship accounted for in your regression. Contrary to the "r" in Peason, where the positive or negative sign denotes the direction of the relationship, the squared "R" value of a Multiple Linear Regression may have both positive and negative terms in the equasion(see the beta coefficients), therefore, the squared "R" is your representation of the correlation.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Is there a correlation coefficient for multiple linear regression ?
Thank you @Elvic_OngGX and @txnelson for helping me out here.
Yes, indeed @txnelson, I was trying to look for a "single" Pearson correlation coefficient for multiple linear regression. I was hoping to make a multiple linear regression analysis "easier" to understand for medical people like me, as I have a number of simple linear regression models with R2adj and Pearson correlation coefficient (Pearson always > R2adjusted) and the term correlation "appeals" more for readers than proportion of variance.
Many thanks to both of you ! Marc
Recommended Articles
- © 2026 JMP Statistical Discovery LLC. All Rights Reserved.
- Terms of Use
- Privacy Statement
- Contact Us