- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Discussions
Solve problems, and share tips and tricks with other JMP users.- JMP User Community
- :
- Discussions
- :
- Re: Is it possible to solve differential equations in JMP ?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Is it possible to solve differential equations in JMP ?
Hello All ,
I would like to know if it is possible to solve differential equations in JMP ? If yes - can you please post an example showing how to do it or provide any blog posts that explain this ? If no - can some one explain why not ?
Note : I do not wish to invoke Matlab to achieve this .
Best
Uday
Uday
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Is it possible to solve differential equations in JMP ?
There is a section in the JSL Scripting Guide
Help==>Books==>Scripting Guide
that deals with the calculation of derivatives. In the JMP 12 Scripting Guide, it starts on page 265.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Is it possible to solve differential equations in JMP ?
There is a section in the JSL Scripting Guide
Help==>Books==>Scripting Guide
that deals with the calculation of derivatives. In the JMP 12 Scripting Guide, it starts on page 265.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Is it possible to solve differential equations in JMP ?
There are at least two ways to calculate a derivative or at least save the formula for the first derivative.
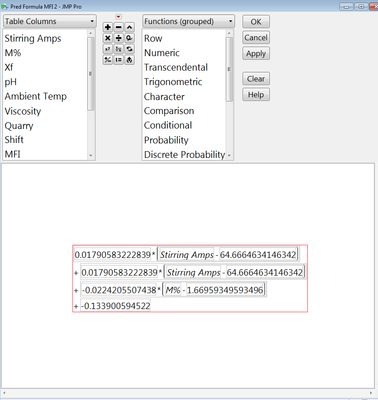
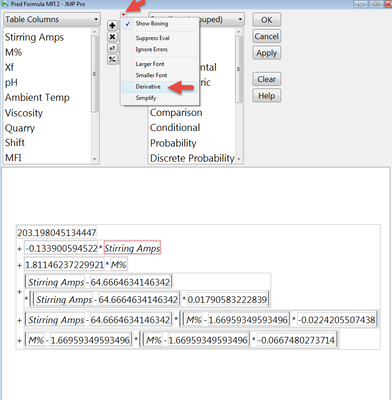
For the first way you need to save a formula or create a formula column. To take the derivative go to the column of interest, right click on the column header and then click Formula. When the formula editor opens you will see the formula and you must select which variable you want to take your derivative with respect to.
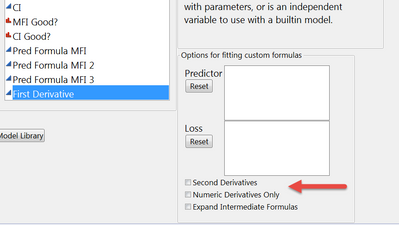
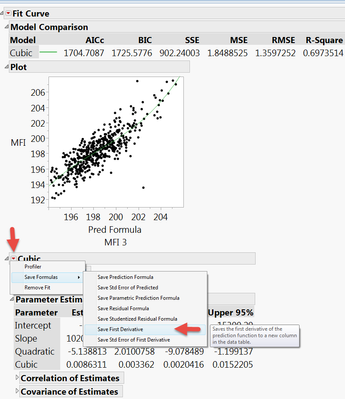
The second way is in the nonlinear platform. You again need to create a model, but instead of saving the prediction formula you will save the formula for the first derivative.
You can also specify that you want second derivatives and/or numeric only derivatives in the nonlinear platform model dialogue.
HTH
Bill
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Is it possible to solve differential equations in JMP ?
JSL has a derivative function. I've forgotten all my calculus, so I can't explain the last three terms, but I made a small test harness, and it works.
// make a really ugly formula
fx = Expr(
A * x ^ W + B * x ^ Z + C * x + D * Sin( E * x ) + F * x * Log( G * x ) + Tan( x ) * Exp( x )
);
// ask JMP to find the derivative with respect to x. p for prime.
fxp = Derivative( Name Expr( fx ), x );
W * x ^ (W - 1) * A
+ Z * x ^ (Z - 1) * B
+ C
+ E * Cosine( E * x ) * D
+ F * Log( G * x ) + G / (G * x) * F * x
+ 1 / Cosine( x ) ^ 2 * Exp( x ) + Exp( x ) * Tan( x )
Test harness:
A = 3;
B = 4;
C = 5;
D = 6;
E = 7;
F = 8;
G = 9;
W = 10;
Z = 11;
// do a small test at some point, "center"
center = 7;
// evaluate the original formula to calculate the slope on a small interval
interval = .0000001;
halfinterval = interval / 2;
x = center - halfinterval;
y1 = fx; // low side of center
x = center + halfinterval;
y2 = fx; // high side of center
slope = (y2 - y1) / interval; // approximate derivative
Write( "\!nslope: " || Char( slope ) );
x = center; // midpoint
yd = fxp; // exact derivative
Write( "\!nderivative: " || Char( yd ) );
Write( "\!npercent error: " || Char( 100 * (slope - yd) / ((slope + yd) / 2) ) );
slope: 13639522056.5796
derivative: 13639522109.8688
percent error: -0.000000390696846545
pretty steep! centers much closer to zero are less steep.
Recommended Articles
- © 2026 JMP Statistical Discovery LLC. All Rights Reserved.
- Terms of Use
- Privacy Statement
- Contact Us