- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Discussions
Solve problems, and share tips and tricks with other JMP users.- JMP User Community
- :
- Discussions
- :
- Re: Interpreting MANOVA repeated measure
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Interpreting MANOVA repeated measure
Hello awesome people!
For the first time in my life, I've tried MANOVA in JMP! I've attached the file with MANOVA analysis saved to the data table. For some reason, I could not save the Response Specification (which I set to Repeated Measures) * If anyone knows how to save this setting as well, please enlighten me..
I need help with answering 2 questions.
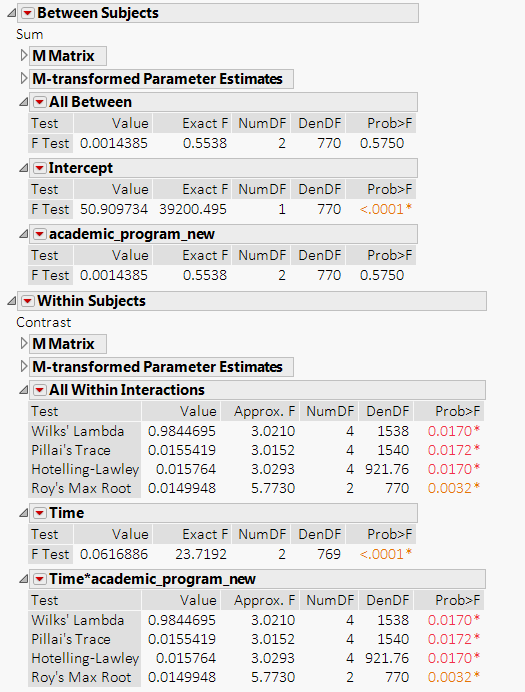
1. I am looking at if there is a difference in the change between three academic groups. Which column do I look for? For sure, there is the effect of time.
However, I'm confused whether I should look at [All Between] and [academic_program_new] column under Between Subjects or at [Time*academic_program_new] column under Within Subjects.
2. How do I calculate partial eta sqaure. I don't mind manual calculation but I don't see any SS error.
Thank you in advance!
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Interpreting MANOVA repeated measure
You're welcome! I'm glad it helped.
Yes, the add-in I wrote calls the *identical* linear mixed-effects model analysis (fit via REML). JMP can already fit these models via the Fit Model dialog (as you saw), so all this add-in does is recruit this platform after defining your effects for you. The main reason I wrote the add-in is to simplify setting up these models when you have several within- and/or between-subject factors that are crossed factorially. In these cases, it can get a bit cumbersome to define all the correct model effects and interactions, so I thought it would be useful to have an add-in that takes care of that. I certainly cannot take credit for the code that fits these models! That magic is performed by the downright amazing team of developers who create JMP.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Interpreting MANOVA repeated measure
Hi @seoleelvjs,
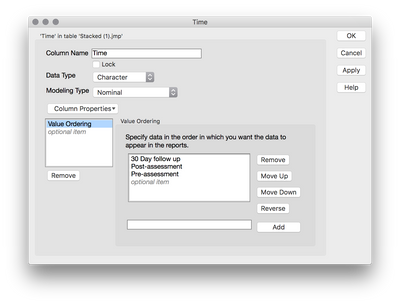
Certainly not pestering me! The ordering of levels for plots and analyses (JMP-wide) is based on the Value Ordering property for the column of interest; if no ordering is specifically defined by you, the levels of that column are ordered alphabetically by default. To override the default alphabetical ordering so you can specify an ordering that is useful for your situation, right-click the column in the table, and go to Column Info. Once you're in Column Info for the Time column, click on the Column Properties drop down on the bottom left and select "Value Ordering." This will reveal the Value Ordering control panel in Column Info (shown below). You can now rearrange your column levels. This change will not only affect output from Fit Model, but will affect all output where an order for the levels of the column need to be displayed.
Julian
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Interpreting MANOVA repeated measure
Hi @seoleelvjs,
I was able to run the Manova script in your table and it reproduced the repeated response you specified just fine. You'll see that jsl in your saved script:
Response Function( "Sum", Repeated( 1 ), Title( "Between Subjects" ) ),
Response Function(
"Contrast",
Repeated( 2 ),
Prefix( "Time*" ),
Title( "Within Subjects" )
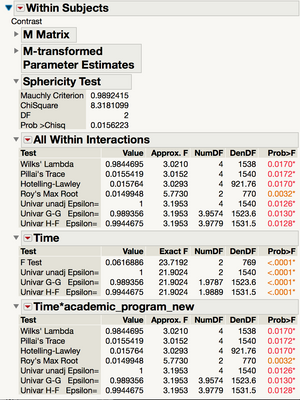
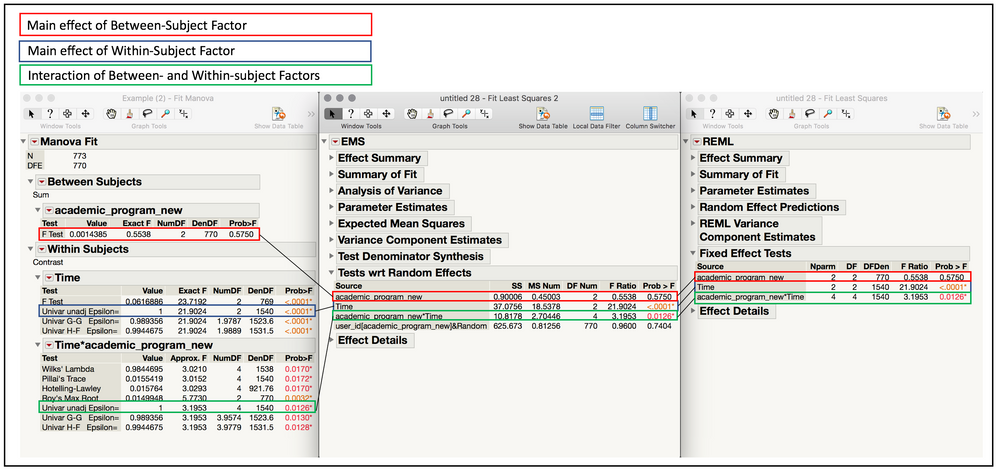
)As for interpretation, I know the output from Manova seems a bit verbose, but once you know where to look it'll be easy! For your within-subject effect of Time (whether there is evidence that the means differ from pre/post/30day, averaging over academic program) look in the time section for your F and associated DF and p value:
For your test of academic program (whether the means for the programs differ, averaging over time), look in the between-subjects section under "academic_program_new":
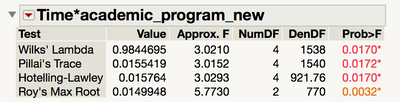
For the interaction between your within and between subjects factors, the test of whether you have evidence the time effect differs for the different academic programs (or equivalently, whether you have evidence that the academic program difference is different and different time points), look in the Within-Subjects section under Time*academic_program_new, and choose your favorite multivariate f statistic to use (whatever is most common in your field -- I would guess Lambda):
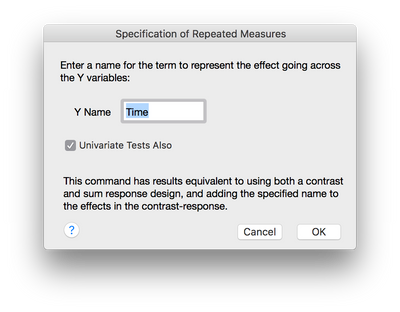
A few additional notes before we get to calculating partial eta squared. The output you requested is for the true multivariate analysis of variance where we are constructing a linear contrast across the multiple within-subject responses. These tests are not the traditional univariate repeated measures tests. If you wish to request the univariate repeated measures tests (what you might get from SPSS repeated measures) you can do so when you call the repeated contrast -- simply check the box for univariate tests also:
When you do this, you will receive additional output in each section. Notice for each of your within-subject tests, there are Univar tests, both uncorrected and epsilon corrected. There is also the familiar Sphericity Test.
Now, to your final question about partial eta squared. You won't be able to get the particular values you need from this output, but you will with a slight restructuring of your data and then by running this model through Fit Model a different way.
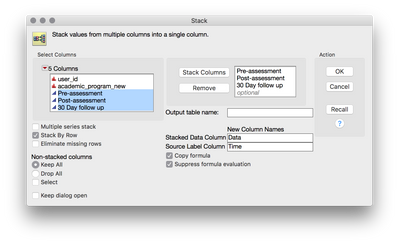
First, we'll use Tables > Stack to Stack your data. We'll tell jmp to stack your three time columns, and then label the columns appropriately in the dialog:
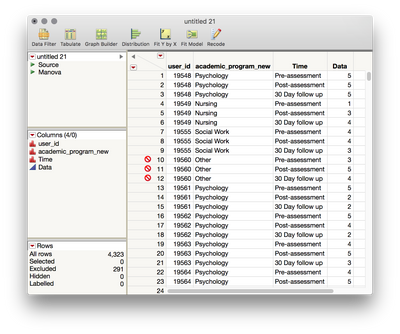
This returns a table where your repeated measurements are across rows rather than separate columns (dataset attached here):
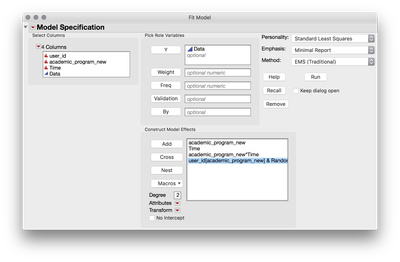
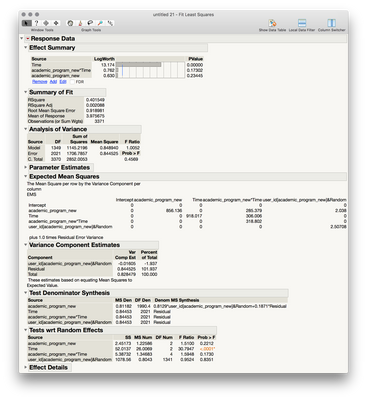
Next, we'll return to Analyze > Fit Model, but rather than specifying multiple Y columns, we'll define your repeated structure completely in the model effects section, and we'll utilize your user_id column to tell JMP there is a random effect present. To do this, we'll first add a full factorial of your "fixed" effects, academic program and time, and then we'll add user_id, and with it selected click the red triangle next to attributes, and select random. This will tell JMP that this effect is a random effect (which is what subjects always are). To be completely formal we need to tell jmp that your subjects are nested inside of the between subjects conditions, so we select the user_id factor in the model effects, and then select academic program in the columns list, and then click "nest." Finally, if you wish to run this model in a way that gives you SS for your calculation of eta squared, change the "Method" at the top right to EMS Traditional (I'll come back to this choice in a minute). Your dialog should look like this:
When you click Run, you'll obtain the traditional expected mean squares repeated measures output with all the terms you need to calculate partial eta squared:
By changing your method to EMS, you were telling JMP to calculate this model using expected mean squares, a traditional and older way of fitting these repeated measures models. The original default, REML, is the much preferred (for many statistical reasons) method for these models, and would return a linear mixed effects models. If you have complete data, a mixed model and ems model will return identical p-values. When there are missing data (at random) the mixed model will outperform EMS. For this and other reaons I would certainly recommend REML over EMS, though you will not be able to calculate an easy effect size measure for your factors (you can read up on the controversy over effect sizes in mixed effects models if you're interested).
If you wish to simplify the specification of these repeated measures models via a mixed model approach, you can download my Full-Factorial Repeated Measures Add-in here: Repeated Measures Add-In. The only requirement is that your data be in tall/stacked form (what we did above).
I hope this helps!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Interpreting MANOVA repeated measure
Hi again @seoleelvjs,
As a follow-up, I thought I should mention that in your case, since you don't have complete data (there are missing observations for certain timepoints for some of your subjects) that the results from these different analyses will not be the same. Because each analysis is approaching the data in a different way the missingness is handled differently, which leads to different results. Just so you can see the relationship of these methods (and the connection between where the relevant results are in each output), I created a version of your dataset removing all subjects with any missing data (so we have complete data for all individuals). When we run these three analyses (MANOVA, EMS, REML) you'll see we get identical results. Below is a screenshot with the relevant areas marked up. I hope this helps!
-julian
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Interpreting MANOVA repeated measure
Thank you so much for the detailed solution and a thorough step-by step explanation! I greatly appreciate it...
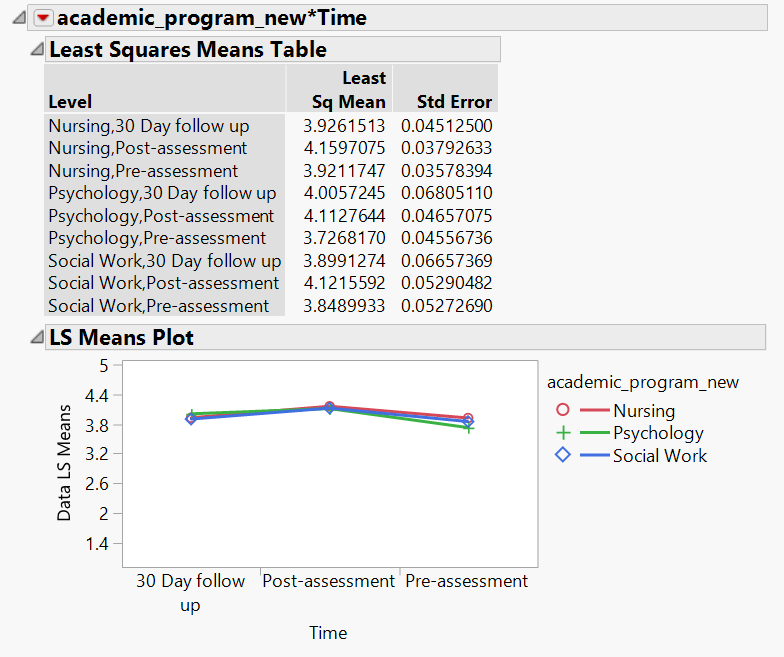
I've tried the three (REML, EMS and MANOVA) without deleting the subjects with missing data and each gave different result, which makes sense as you have explained. I won't hesitate to take your advice on using REML over EMS...It seems REML shows a more accurate depiction of the relationship (which I can tell from just looking at the LS means plot...it looks like there is only a slight difference in LS means between the group at different periods of time) than MANOVA, and more resilient to missing data.
Last question, are REML and the add-in you provided essentially the same model?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Interpreting MANOVA repeated measure
You're welcome! I'm glad it helped.
Yes, the add-in I wrote calls the *identical* linear mixed-effects model analysis (fit via REML). JMP can already fit these models via the Fit Model dialog (as you saw), so all this add-in does is recruit this platform after defining your effects for you. The main reason I wrote the add-in is to simplify setting up these models when you have several within- and/or between-subject factors that are crossed factorially. In these cases, it can get a bit cumbersome to define all the correct model effects and interactions, so I thought it would be useful to have an add-in that takes care of that. I certainly cannot take credit for the code that fits these models! That magic is performed by the downright amazing team of developers who create JMP.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Interpreting MANOVA repeated measure
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Interpreting MANOVA repeated measure
Sorry to keep pestering you, but just one quick question.
The LS means plot gives a somewhat reversed name of time points, as you can see below. The proper way of presentation would be pre > post > 30 day...
Below is the JSL. Is there some kind of setting that I am unaware of?
Fit Model(
Y( :Data ),
Effects( :academic_program_new, :Time, :academic_program_new * :Time ),
Random Effects(
:user_id[:academic_program_new],
:user_id * :Time[:academic_program_new]
),
NoBounds( 1 ),
Personality( "Standard Least Squares" ),
Method( "REML" ),
Emphasis( "Minimal Report" ),
Run(
:Data << {Analysis of Variance( 0 ), Lack of Fit( 0 ),
Plot Actual by Predicted( 0 ), Plot Regression( 0 ),
Plot Residual by Predicted( 0 ), Plot Effect Leverage( 0 ),
{:academic_program_new << {LSMeans Table( 0 )}, :academic_program_new *
:Time << {LSMeans Plot( 1 )}}}
),
SendToReport(
Dispatch( {"Response Data"}, "Effect Details", OutlineBox, {Close( 0 )} )
)
)
Thank you in advance!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Interpreting MANOVA repeated measure
Hi @seoleelvjs,
Certainly not pestering me! The ordering of levels for plots and analyses (JMP-wide) is based on the Value Ordering property for the column of interest; if no ordering is specifically defined by you, the levels of that column are ordered alphabetically by default. To override the default alphabetical ordering so you can specify an ordering that is useful for your situation, right-click the column in the table, and go to Column Info. Once you're in Column Info for the Time column, click on the Column Properties drop down on the bottom left and select "Value Ordering." This will reveal the Value Ordering control panel in Column Info (shown below). You can now rearrange your column levels. This change will not only affect output from Fit Model, but will affect all output where an order for the levels of the column need to be displayed.
Julian
Recommended Articles
- © 2026 JMP Statistical Discovery LLC. All Rights Reserved.
- Terms of Use
- Privacy Statement
- Contact Us