How to interpret odds-ratios for ordinal logistic regression with multiple levels for dependent variable

[#1]

I have an ordinal dependent variable practically composed of 5 levels. I am fitting a logistic model with three continuous parameters derived using factor analysis. I am having some trouble understanding the effect summary with respect to the odds-ratio associated with each level.

JMP 14 gives parameters estimates for 4 intercepts and 1 coefficient estimate for each variable. My question is why does the model report only 1 estimate for each variable and not four for each intercept/level threshold.

I reckon this has something to do with the cumulative nature of the logits in ordinal logistic models, correct? How can I interpret the odds-ratios I derive from my coefficient estimates in simple language with regard to the effect of achieving higher levels on my DV?  

For reference I'll share my ORs. OR1= -1.773 (p=0.002), OR2= 0.0455 (p=0.84), OR3= -4.07 (p=<0.0001)

Thank you


Link to a related post

[#2]

Hi @adamszymanski,

  Good posts, and I've been following your other thread as well. Very interesting discussion topics. It might be good to also link this thread to your other discussion about logistic regression.

  If you're now fitting the ordinal variable with the PCA components, then understanding the odds ratio will be a little complicated as the PCA axes are linear combinations of the original factors.

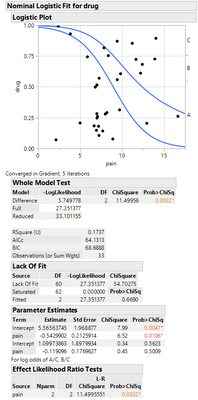
  The linear function for a given ordinal level requires only a slope and intercept. Those are then transformed to probabilities by taking the logistic function: 1/(1+exp(x)). You can see this example, and maybe better understand the transformations/interpretation using the Analgesics.jmp data table in the help files. If you do a logistic regression of drug[A, B, C] vs pain, you'll get to look over the equations. Notice that the Prob[x] functions all add up to one, meaning you get the probability the answer is A, or B, or C, and since the probability has to total 1, Prob[C] is basically 1-Prob[A]-Prob[B].

  As for the odds ratio, I think it might be calculating the logit or log-odds since you have a negative value, but I'm not 100% sure on that. In general, though the odds ratio is the ratio of odds event 1 happening in the presence of event 2 divided by the odds of event 1 in the absence of event 2.

  Since I think JMP is reporting the log-odds, you'd have to transform that number back to get the odds ratio. In your case:

log-odds1 = -1.773 -> OR1 = exp(-1.773) = 0.1698 ~ 17/100 odds ratio

log-odds2 = 0.0455 -> OR2 = exp(0.0455) = 1.047 ~105/100 odds ratio

log-odds3 = -4.07 -> OR3 = exp(-4.07) = 0.0171 ~ 2/100 odds ratio

  However, interpreting these as principle components is rather complicated and not so straight forward. To really interpret it, you'd need to know what kind of odds you're comparing, and if it's principle components, that's complicated.

  As an example, say you have 100 red cars, of which 35 got speeding tickets the previous month. During that same time period, you also had 100 blue cars, of which 15 got speeding tickets. The odds of red cars getting tickets is 35 to 65 or 35:65 = 0.54, for blue cars, it's 15:85 = 0.18. The odds ratio is 0.54/0.18 = 3.1. So red cars have 3.1-times the odds of getting a ticket, but (35/100)/(15/100) = 2.3-times as likely to get a ticket. The log-odds would then be: ln(3.1) = 1.12. I think JMP is reporting the 1.12, log-odds value.

Hope this helps.

DS

[#3]

Thanks DS,

My apologies, I should have been more clear with my calculations. The ORs I posted were calculated from the coefficient results on each of the variables (is that the same as the log-odds?). With the coefficients that were negative I assumed that you simply calculated exp(x) using the absolute value and then kept the negative as some aspect of direction of magnitude. I can see now why you wouldn't do that, thanks for helping clear that up. 

My coefficients (or log odds?) are 

X1= -0.54,

X2=0.0455,

X3= -1.4038

which then give ORs of 0.58, 1.05, and 0.25 respectively, or 58/100, 105/100, and 25/100

If I've already written about the information about which variables each of the components are primarily determined by, then is it not as simple as treating these components as any other continuous variable? How would I go about determining what odds I'm comparing?

In your example the outcome set is binary and the odds-ratios make clear sense. What would the odds-ratio mean when there are 3 or more ordinal outcomes? Generally speaking, would they represent some kind of magnitude in terms of the odds of moving up or down on a scale of ordered outcomes? Are the ratio's compared against each other or a specific outcome (for instance, the odds of remaining on level 1 as opposed to moving to levels 2,3,4,5)?

[#4]

Hi @adamszymanski,

  The parameter estimates for the terms would be the log odds

  Since this is in relation to your other posts, are you actually using the principle components to fit? If so, you'll want to use the least number of eigenvectors to do so. You can view their cumulative percent contribution in the PCA platform and select the number of PCs that add up to at least 85%, but you don't need to do all of them. Save the PCs to the data table and refit the ordinal logistic model using the PCs instead of the original X's. Keep in mind that when you do that, each principle component is a linear combination of X's. For example, Prin1 = a*X1+b*X2+c*X3 and Prin2 = d*X1+e*X2+f*X3. The coefficients in front of each X can take on positive or negative values, whichever is needed to maximize the variance in the data along that PC.

  If you are then fitting using the PCs, you would be evaluating the log odds for the PCs and not the original Xs.

  In the example I mentioned earlier using Analgesics, there are three levels to :drug with the continuous factor :pain. The Parameter Estimates table gives the log odds for A/C and B/C, so it's comparing the log odds of drug A to drug C and drug B to drug C. Here, if finds the log odds A/C = -0.543, which means the odds pain reported with drug A is 0.947 lower than the odds of pain reported with drug C (drug A is more effective).

  Another good example, although not ordinal is the Titanic Passengers.jmp file. If you do a logistic fit of Survived (Y/N) by Passenger Class, Sex, Age, Siblings and Spouses, and Port, you get a nice example of how to interpret the results. Here, the parameter estimate for Passenger Class[2-1] is -1.127, so the log odds is -1.127, or the overall odds of surviving in class 2 was exp(-1.127)=0.324 lower than the odds surviving in class 1. You can view the odds ratio by going to the red triangle under Nominal Logistic Fit and selecting that option. And indeed, you see the odds ratio of class 2/class 1 is 0.324. So, in this case you get to see the odds ratio for all the pairwise combinations of Passenger Class, Sex, and Port. Another example is Sex: the odds ratio of females surviving is 13.9 to the odds of males surviving.

  You might want to check if you have the Odds Ratios option available. This was not available for the Analgesics example. 

  For your case, if you don't have the Odds Ratios available, it sounds like you'll have to calculate it for each pairing of levels.

Hope this helps.

DS

[#5]

Yes the above results are in reference to fitting three pc's which explain a little more than 85% variance. 

Thanks for the examples, I think I am beginning to understand and I will dig into the data file you've provided when I have more time.

In my case, with multiple ordinal DV levels how am I able to determine which outcome I am comparing my odds ratios against? 

For example, my principle component 1 is termed "institutional scale" and is determined by continuous variables. The log odds for this component are -0.5444 which gives odds ratio, exp(-0.544)= 0.5801. Does this ratio then relate to unit changes in my component? Are the odds-ratios representing some averaged odds of achieving higher levels on my DV? Such that the averages of the data for institutional scale give 58/100 odds of higher levels?

Thank you

[#6]

Would it be correct to say that one can use the coefficient estimates for each of the factors and estimating their respective odds-ratios we can indicate the direction and magnitude on the effect each factor has on the likelihood of the lowest outcome?

[#7]

Have you saved the model as a column formula? JMP will create a series of columns. The first column is the linear predictor for computing the cumulative logits. This result is then used in the next several columns to compute the probability of the individual levels. You should be able to use these results to compute any odds or odds ratios you need without any ambiguity.

Also, the Prediction Profiler is a good tool for computing the probability for any condition. You can using it in the fitting platform or as a stand-alone platform using the saved column formulas mentioned above.

[#8 · Accepted solution]

Hi @adamszymanski,

  As @Mark_Bailey mentioned, you should save the prediction formulas to the data table and calculate the odds ratio directly. When you calculate the odds ratio, it will always be between two events, of which you can define when you calculate the odds ratio manually. As with the Analgesics example, it was evaluating the log odds for drug A to drug C and drug B to drug C.

  In your case, you can keep the odds ratio as a comparison of odds of the principle components, but then to use that as a predictive evaluation, you would need to convert your original X's into the PCs by using the eigenvector coefficients from the PCA analysis. This is not always so straightforward to do as you need to transform the original vectors to your PCs and make sure you normalize them appropriately. But, it's possible. It might be easier to do compared to transforming your log odds to the original X's and then use that as a predictive evaluation.

  Just be sure to be cautious in that some kind of transformation is needed from either X's -> PCAs or PCAs -> X's (that is, if you prefer using PCAs in the model). You'll have to keep that in mind because you collect data on the X's, not the PCAs.

Good luck!,

DS